
【题目】已知函数![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)已知![]() 在
在![]() 处的切线与
处的切线与![]() 轴垂直,若方程
轴垂直,若方程![]() 有三个实数解
有三个实数解![]() 、
、![]() 、
、![]() (
(![]() ),求证:
),求证:![]() .
.
【答案】(1)①当![]() 时,
时, ![]() 在
在![]() 单调递增,②当
单调递增,②当![]() 时,
时,![]() 单调递增区间为
单调递增区间为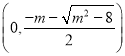 ,
,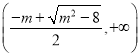 ,单调递减区间为
,单调递减区间为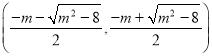
(2)证明见解析
【解析】
(1)先求解导函数,然后对参数![]() 分类讨论,分析出每种情况下函数
分类讨论,分析出每种情况下函数![]() 的单调性即可;
的单调性即可;
(2)根据条件先求解出![]() 的值,然后构造函数
的值,然后构造函数![]() 分析出
分析出![]() 之间的关系,再构造函数
之间的关系,再构造函数![]() 分析出
分析出![]() 之间的关系,由此证明出
之间的关系,由此证明出![]() .
.
(1)![]() ,
,![]()
①当![]() 时,
时,![]() 恒成立,则
恒成立,则![]() 在
在![]() 单调递增
单调递增
②当![]() 时,令
时,令![]() 得
得![]() ,
,
解得![]() ,
,![]()
又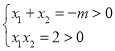 ,∴
,∴![]()
∴当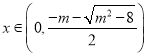 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当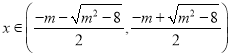 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当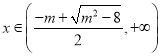 时,
时,![]() ,
,![]() 单调递增.
单调递增.
(2)依题意得,![]() ,则
,则![]()
由(1)得,![]() 在
在![]() 单调递增,在
单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
∴若方程![]() 有三个实数解
有三个实数解![]() ,
,
则![]()
法一:双偏移法
设![]() ,则
,则![]()
∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,
,![]()
∴![]() ,即
,即![]()
∵![]() ,∴
,∴![]() ,其中
,其中![]() ,
,![]()
∵![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() ,即
,即![]()
设![]() ,
,![]()
∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,
,![]()
∴![]() ,即
,即![]()
∵![]() ,∴
,∴![]() ,其中
,其中![]() ,
,![]()
∵![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,即
,即![]()
∴![]() .
.
法二:直接证明法
∵![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
∴要证![]() ,即证
,即证![]()
设![]() ,则
,则![]()
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
∴![]() ,
,![]()
∴![]() ,即
,即![]()
(注意:若![]() 没有证明,扣3分)
没有证明,扣3分)
关于![]() 的证明:
的证明:
(1)![]() 且
且![]() 时,
时,![]() (需要证明),其中
(需要证明),其中![]()
∴![]()
∴![]()
∴![]()
(2)∵![]() ,∴
,∴![]()
∴![]() ,即
,即![]()
∵![]() ,
,![]() ,∴
,∴![]() ,则
,则![]()
∴![]()


科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() 为正三角形,平面
为正三角形,平面![]() 平面
平面![]() ,
,![]() 是线段
是线段![]() 的中点,
的中点,![]() 是线段
是线段![]() 上的动点.
上的动点.
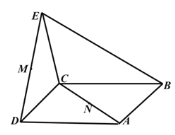
(1)探究![]() 四点共面时,
四点共面时,![]() 点位置,并证明;
点位置,并证明;
(2)当![]() 四点共面时,求
四点共面时,求![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项等比数列{an}满足a1=2,2a2=a4﹣a3,数列{bn}满足bn=1+2log2an.
(1)求数列{an},{bn}的通项公式;
(2)令cn=anbn,求数列{cn}的前n项和Sn;
(3)若λ>0,且对所有的正整数n都有2λ2﹣kλ+2![]() 成立,求k的取值范围.
成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的各项均为正数,记数列
的各项均为正数,记数列![]() 的前n项和为
的前n项和为![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)求数列![]() 的通项公式;
的通项公式;
(3)若![]() ,且
,且![]() 成等比数列,求k和t的值.
成等比数列,求k和t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为评估两套促销活动方案(方案1运作费用为5元/件;方案2的运作费用为2元件),在某地区部分营销网点进行试点(每个试点网点只采用一种促销活动方案),运作一年后,对比该地区上一年度的销售情况,制作相应的等高条形图如图所示.
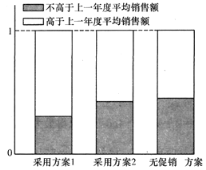
(1)请根据等高条形图提供的信息,为该公司今年选择一套较为有利的促销活动方案(不必说明理由);
(2)已知该公司产品的成本为10元/件(未包括促销活动运作费用),为制定本年度该地区的产品销售价格,统计上一年度的8组售价![]() (单位:元/件,整数)和销量
(单位:元/件,整数)和销量![]() (单位:件)
(单位:件)![]() 如下表所示:
如下表所示:
售价 | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
销量 | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
①请根据下列数据计算相应的相关指数![]() ,并根据计算结果,选择合适的回归模型进行拟合;
,并根据计算结果,选择合适的回归模型进行拟合;
②根据所选回归模型,分析售价![]() 定为多少时?利润
定为多少时?利润![]() 可以达到最大.
可以达到最大.
|
|
| |
| 52446.95 | 13142 | 122.89 |
| 124650 | ||
(附:相关指数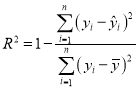 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角),以坐标原点
的倾斜角),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 时直线
时直线![]() 的普通方程;
的普通方程;
(2)直线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为 为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=asinθ(a≠0).
为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=asinθ(a≠0).
(1)求圆C的直角坐标方程与直线l的普通方程;
(2)设直线l截圆C的弦长是半径长的![]() 倍,求a的值.
倍,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() ,F为焦点,
,F为焦点,![]() 面积为1.
面积为1.
(1)求抛物线C的方程;
(2)过点P引圆![]() 的两条切线PA、PB,切线PA、PB与抛物线C的另一个交点分别为A、B,求直线AB斜率的取值范围.
的两条切线PA、PB,切线PA、PB与抛物线C的另一个交点分别为A、B,求直线AB斜率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com