
数列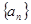 满足:
满足: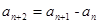 (
(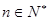 ),且
),且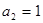 ,若数列的前2011项之和为2012,则前2012项的和等于
,若数列的前2011项之和为2012,则前2012项的和等于
A.0 B. 1 C.2012 D.2013
D
【解析】
试题分析:假设首项设a1=m,由于a2=1,且an+2=an+1-an∴a3=1-m.a4=-m,a5=-1,a6=m-1,a7=m,a8=1,a9=1-m…,∴数列{an}是周期为6的周期函数,且前6项和为0,∴数列的前2011项之和为m⇒m=2012,2011=6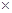 335+1,2012=6
335+1,2012=6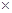 335+2,则前2012项的和等于2012+1=2013.故选D.
335+2,则前2012项的和等于2012+1=2013.故选D.
考点:本题主要考查由递推公式推导数列的通项公式,其中渗透了周期数列这一知识点,属于基础题.
点评: 解决该试题的关键是可通过递推公式求出数列的前九项,从而确定数列周期为6,再由数列周期从而求解a2011=a1,求出结果.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
(09年大丰调研)(16分)
已知函数![]() ,数列
,数列![]() 满足对于一切
满足对于一切![]() 有
有![]() ,且
,且![]() .数列
.数列![]() 满足
满足![]() ,设
,设![]() .
.
(Ⅰ)求证:数列![]() 为等比数列,并指出公比;
为等比数列,并指出公比;
(Ⅱ)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(Ⅲ)若![]() (
(![]() 为常数),求数列
为常数),求数列![]() 从第几项起,后面的项都满足
从第几项起,后面的项都满足![]() .
.
查看答案和解析>>
科目:高中数学 来源:2011—2012学年度湖北省天门中学高三上学期期中理科数学考试试卷 题型:解答题
在数列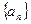 中,
中,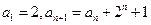
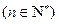 .
.
(Ⅰ)求证:数列 为等差数列;
为等差数列;
(Ⅱ)设数列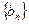 满足
满足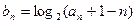 ,若
,若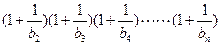
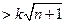 对一切
对一切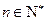 且
且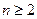 恒成立,求实数
恒成立,求实数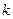 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com