
【题目】如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心(事件A)的概率是![]() ,取到方块(事件B)的概率是
,取到方块(事件B)的概率是![]() ,问:
,问:
(1)取到红色牌(事件C)的概率是多少?
(2)取到黑色牌(事件D)的概率是多少?
科目:高中数学 来源: 题型:
【题目】2016年入冬以来,各地雾霾天气频发, ![]() 频频爆表(
频频爆表(![]() 是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与
是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与![]() 的浓度是否相关,某市现采集周一到周五某一时间段车流量与
的浓度是否相关,某市现采集周一到周五某一时间段车流量与![]() 的数据如下表:
的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 69 | 70 | 74 | 78 | 79 |
(1)请根据上述数据,在下面给出的坐标系中画出散点图;
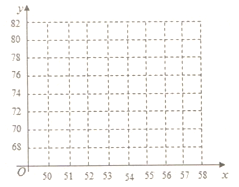
(2)试判断![]() 与
与![]() 是否具有线性关系,若有请求出
是否具有线性关系,若有请求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,若没有,请说明理由;
,若没有,请说明理由;
(3)若周六同一时间段的车流量为60万辆,试根据(2)得出的结论,预报该时间段的![]() 的浓度(保留整数).
的浓度(保留整数).
参考公式: 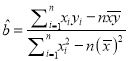
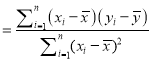 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线![]() 上的点
上的点 对应的参数
对应的参数![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若点![]() ,
, ![]() 在曲线
在曲线![]() 上,求
上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学从参加高一年级上学期期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)估计这次考试的及格率(60分及以上为及格).
(2)从成绩是70分以上(包括70分)的学生中选一人,求选到第一名学生的概率(第一名学生只一人).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水![]() (单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药
(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药![]() (单位:微克)的统计表:
(单位:微克)的统计表:

(1)令![]() ,利用给出的参考数据求出
,利用给出的参考数据求出![]() 关于
关于![]() 的回归方程
的回归方程![]() .(
.(![]() ,
,![]() 精确到0.1)
精确到0.1)
参考数据:![]() ,
,![]() ,
,![]()
其中![]() ,
,![]()
(2)对于某种残留在蔬菜上的农药,当它的残留量不高于20微克时对人体无害,为了放心食用该蔬菜,请估计至少需用用多少千克的清水清洗1千克蔬菜?(精确到0.1,参考数据![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
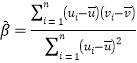 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4月16日摩拜单车进驻大连市旅顺口区,绿色出行引领时尚,旅顺口区对市民进行“经常使用共享单车与年龄关系”的调查统计,若将单车用户按照年龄分为“年轻人”(20岁~39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,抽取一个容量为200的样本,将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”。使用次数为5次或不足5次的称为“不常使用单车用户”,已知“经常使用单车用户”有120人,其中![]() 是“年轻人”,已知“不常使用单车用户”中有
是“年轻人”,已知“不常使用单车用户”中有![]() 是“年轻人”.
是“年轻人”.
(1)请你根据已知的数据,填写下列![]() 列联表:
列联表:
年轻人 | 非年轻人 | 合计 | |
经常使用单车用户 | |||
不常使用单车用户 | |||
合计 |
(2)请根据(1)中的列联表,计算![]() 值并判断能否有
值并判断能否有![]() 的把握认为经常使用共享单车与年龄有关?
的把握认为经常使用共享单车与年龄有关?
(附: 
当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关;当
有关;当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关;当
有关;当![]() 时,认为事件
时,认为事件![]() 与
与![]() 是无关的)
是无关的)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com