
【题目】已知中心在原点的椭圆C的左焦点F(﹣ ![]() ,0),右顶点A(2,0).
,0),右顶点A(2,0).
(1)求椭圆C的标准方程;
(2)斜率为 ![]() 的直线l与椭圆C交于A、B两点,求弦长|AB|的最大值及此时l的直线方程.
的直线l与椭圆C交于A、B两点,求弦长|AB|的最大值及此时l的直线方程.
【答案】
(1)解:由题意可知:c= ![]() ,a=2,∴b2=a2﹣c2=1.
,a=2,∴b2=a2﹣c2=1.
∵焦点在x轴上,
∴椭圆C的方程为: ![]()
(2)解:设直线l的方程为y= ![]() x+b,由
x+b,由 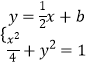 ,
,
可得x2+2bx+2b2﹣2=0,
∵l与椭圆C交于A、B两点,
∴△=4b2﹣4(2b2﹣2)≥0,即b2≤2.
设A(x1,y1),B(x2,y2),
则x1+x2=﹣2b,x1x2=2b2﹣2.
∴弦长|AB|= ![]() =
= ![]() ,
,
∵0≤b2≤2,
∴|AB|= ![]() ≤
≤ ![]() ,
,
∴当b=0,即l的直线方程为y= ![]() x时,弦长|AB|的最大值为
x时,弦长|AB|的最大值为 ![]()
【解析】(1)由已知根据椭圆的简单性质可求出a、b的值进而得到椭圆的方程。(2)联立直线和椭圆的方程得到关于x的一元二次方程,设出A、B两点的坐标根据韦达定理得到x1+x2和x1x2 关系式,代入弦长公式即可求出结果,利用椭圆自身的范围限制得到b的取值范围,进而得到弦长|AB|的最大值以及直线的方程。
【考点精析】认真审题,首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() ).
).


科目:高中数学 来源: 题型:
【题目】脱贫是政府关注民生的重要任务,了解居民的实际收入状况就显得尤为重要.现从某地区随机抽取![]() 个农户,考察每个农户的年收入与年积蓄的情况进行分析,设第
个农户,考察每个农户的年收入与年积蓄的情况进行分析,设第![]() 个农户的年收入
个农户的年收入![]() (万元),年积蓄
(万元),年积蓄![]() (万元),经过数据处理得
(万元),经过数据处理得![]()
(Ⅰ)已知家庭的年结余![]() 对年收入
对年收入![]() 具有线性相关关系,求线性回归方程;
具有线性相关关系,求线性回归方程;
(Ⅱ)若该地区的农户年积蓄在![]() 万以上,即称该农户已达小康生活,请预测农户达到小康生活的最低年收入应为多少万元?
万以上,即称该农户已达小康生活,请预测农户达到小康生活的最低年收入应为多少万元?
附:在![]() 中,
中, 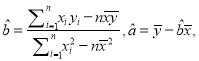 其中
其中![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程![]() .
.
(Ⅰ)若此方程表示圆,求![]() 的取值范围;
的取值范围;
(Ⅱ)若(Ⅰ)中的圆与直线![]() 相交于
相交于![]() ,
, ![]() 两点,且
两点,且![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,求以![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)如果对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() ,使得函数
,使得函数![]() 的最大值为0,若存在,求出
的最大值为0,若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称函数
称函数![]() 的一个上界.已知函数
的一个上界.已知函数![]() ,
, ![]() .
.
(1)若函数![]() 为奇函数,求实数
为奇函数,求实数![]() 的值;
的值;
(2)在第(1)的条件下,求函数![]() 在区间
在区间![]() 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市郊区有一加油站,2018年初汽油的存储量为50吨,计划从年初起每周初均购进汽油![]() 吨,以满足城区内和城外汽车用油需求,已知城外汽车用油每周5吨;城区内汽车用油前
吨,以满足城区内和城外汽车用油需求,已知城外汽车用油每周5吨;城区内汽车用油前![]() 个周需求量
个周需求量![]() 吨与
吨与![]() 的函数关系式为
的函数关系式为![]()
![]() ,
, ![]() 为常数,且前4个周城区内汽车的汽油需求量为100吨.
为常数,且前4个周城区内汽车的汽油需求量为100吨.
(1)试写出第![]() 个周结束时,汽油存储量
个周结束时,汽油存储量![]() (吨)与
(吨)与![]() 的函数关系式;
的函数关系式;
(2)要使16个周内每周按计划购进汽油之后,加油站总能满足城区内和城外的需求,且每周结束时加油站的汽油存储量不超过150吨,试确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AC=AA1=4,AB=3,AB⊥AC.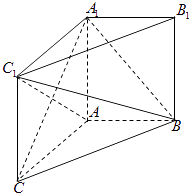
(Ⅰ)求证:A1C⊥平面ABC1;
(Ⅱ)求二面角A﹣BC1﹣A1的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左、右焦点分别为
的左、右焦点分别为 ![]() ,椭圆
,椭圆 ![]() 过点
过点 ![]() ,直线
,直线 ![]() 交
交 ![]() 轴于
轴于 ![]() ,且
,且 ![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求椭圆 ![]() 的方程;
的方程;
(2)设 ![]() 是椭圆
是椭圆 ![]() 的上顶点,过点
的上顶点,过点 ![]() 分别作直线
分别作直线 ![]() 交椭圆
交椭圆 ![]() 于
于 ![]() 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为 ![]() ,且
,且 ![]() ,证明:直线
,证明:直线 ![]() 过定点.
过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com