练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若函数y＝f(x)同时具有下列三个性质：(1)最小正周期为π；(2)图像关于直线x＝对称；(3)在区间上是增函数．则y＝f(x)的解析式可以是

    [　　]
    A．

    y＝sin

    B．

    y＝cos

    C．

    y＝sin

    D．

    y＝cos

    答案：C
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：河北省衡水中学2011－2012学年高二下学期期中考试数学文科试题 题型：022

    对于三次函数f(x)＝ax3＋bx2＋cx＋d(a≠0)，给出定义：(x)是函数f(x)的导函数，(x)是(x)的导函数，若方程(x)＝0有实数解x0，则称点(x0，f(x0))为函数y＝f(x)的“拐点”．某同学经研究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且拐点就是对称中心．若，请你根据这一发现，求：

    (1)函数的对称中心为________．

    (2)＝________．

    查看答案和解析>>

    科目：高中数学 来源：山东省潍坊市2012届高三一轮模拟考试数学理科试题 题型：013

    若直角坐标平面内的两点P、Q满足条件：

    ①P、Q都在函数y＝f(x)的图象上；

    ②P、Q关于原点对称．

    则称点对[P，Q]是函数Y＝f(x)的一对“友好点对”(点对[P，Q]与[Q，P]看作同一对“友好点对”)．已知函数，f(x)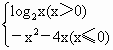＝，则此函数的“友好点对”有

    [　　]

    A．0对

    B．1对

    C．2对

    D．3对

    查看答案和解析>>

    科目：高中数学 来源：山东省东营市2012届高三一模(3月)数学文科试题 题型：013

    若直角坐标平面内的两点P、Q同时满足下列条件：

    ①P、Q都在函数y＝f(x)的图象上；

    ②P、Q关于原点对称．

    则称点对[P，Q]是函数y＝f(x)的一对“友好点对”

    (注：点对[P，Q]与[Q，P]看作同一对“友好点对)．

    已知函数f(x)＝，则此函数的“友好点对”有

    [　　]

    A．0对

    B．1对

    C．2对

    D．3对

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若直角坐标平面内的两点P，Q满足条件：①P，Q都在函数y＝f(x)的图像上；②P，Q关于原点对称．则称点对[P，Q]是函数y＝f(x)的一对“友好点对”(点对[P，Q]与[Q，P]看作同一对“友好点对”)．已知函数f(x)＝则此函数的“友好点对”有                                      (　　)

    A．0对                             B．1对

    C．2对                             D．3对

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年上海交大附中高三数学理总复习二函数的图像与性质练习卷（解析版） 题型：选择题

    若直角坐标平面内的两点P、Q满足①P、Q都在函数y＝f(x)的图像上；②P、Q关于原点对称，则称点对[P，Q]是函数y＝f(x)的一对“友好点对”(注：点对[P，Q]与[Q，P]看作同一对“友好点对”)．

    已知函数f(x)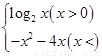＝则此函数的“友好点对”有(　　)

    A．0对    B．1对

    C．2对    D．3对

     

    查看答案和解析>>

    同步练习册答案