
【题目】已知抛物线![]() 的焦点
的焦点![]() 与椭圆
与椭圆![]() 的右焦点重合,抛物线
的右焦点重合,抛物线![]() 的动弦
的动弦![]() 过点
过点![]() ,过点
,过点![]() 且垂直于弦
且垂直于弦![]() 的直线交抛物线的准线于点
的直线交抛物线的准线于点![]() .
.
(Ⅰ)求抛物线的标准方程;
(Ⅱ)求![]() 的最小值.
的最小值.
【答案】(Ⅰ) ![]() (Ⅱ)2
(Ⅱ)2
【解析】
(Ⅰ)由椭圆求得右焦点,根据抛物线的焦点求出p的值,再写出抛物线C的标准方程;
(Ⅱ)①当动弦AB所在的直线斜率不存在时,求得![]() 2;②当动弦AB所在的直线斜率存在时,写出AB所在直线方程,与抛物线方程联立求出弦长|AB|;写出FM所在的直线方程,与抛物线方程联立求出弦长|MF|,再求
2;②当动弦AB所在的直线斜率存在时,写出AB所在直线方程,与抛物线方程联立求出弦长|AB|;写出FM所在的直线方程,与抛物线方程联立求出弦长|MF|,再求![]() 的最小值,从而得出结论.
的最小值,从而得出结论.
(Ⅰ)由椭圆方程得,椭圆的右焦点为![]()
∴抛物线的焦点为![]() ,∴
,∴![]() ,抛物线的标准方程为
,抛物线的标准方程为![]() .
.
(Ⅱ)①当动弦![]() 所在直线的斜率不存在时,易得:
所在直线的斜率不存在时,易得:
![]() ,
,![]() ,
,![]() .
.
②当动弦![]() 所在的直线斜率存在时,易知,
所在的直线斜率存在时,易知,![]() 的斜率不为0.
的斜率不为0.
设![]() 所在直线方程为
所在直线方程为![]() ,且
,且![]() ,
,![]() .
.
联立方程组:![]() ,得
,得![]() ;
;
![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
![]() 所在的直线方程为
所在的直线方程为![]() ,联立方程组:
,联立方程组: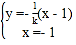 ,得点
,得点![]() ,
,
∴![]()
∴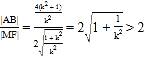 ,
,
综上所述:![]() 的最小值为2.
的最小值为2.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】男生4人和女生3人排成一排拍照留念.
(1)有多少种不同的排法(结果用数值表示)?
(2)要求两端都不排女生,有多少种不同的排法(结果用数值表示)?
(3)求甲乙两人相邻的概率.(结果用最简分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在实数,使得
,若存在实数,使得![]() 成立,则x0称为f(x)的“不动点”.
成立,则x0称为f(x)的“不动点”.
(1)设函数![]() ,求
,求![]() 的不动点;
的不动点;
(2)设函数![]() ,若对于任意的实数b,函数f(x)恒有两相异的不动点,求实数a的取值范围;
,若对于任意的实数b,函数f(x)恒有两相异的不动点,求实数a的取值范围;
(3)设函数![]() 定义在
定义在![]() 上,证明:若
上,证明:若![]() 存在唯一的不动点,则
存在唯一的不动点,则![]() 也存在唯一的不动点.
也存在唯一的不动点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与椭圆
与椭圆![]() 有一个相同的焦点,过点
有一个相同的焦点,过点![]() 且与
且与![]() 轴不垂直的直线
轴不垂直的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)试问直线![]() 是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甜皮鸭,乐山人称卤鸭子,也称嘉州甜皮鸭,是乐山著名美食,起源于乐山市夹江县木城古镇,每年吸引成千上万的外地人前来品尝.某商家生产卤鸭子,每公斤鸭子的成本为![]() 元,加工费为
元,加工费为![]() 元(
元(![]() 为常数),且
为常数),且![]() ,设该商家每公斤卤鸭子的售价为
,设该商家每公斤卤鸭子的售价为![]() 元(
元(![]() ),日销售量
),日销售量![]() (单位:公斤),且
(单位:公斤),且![]() (
(![]() 为自然对数的底数).根据市场调查,当每公斤卤鸭子的出售价为
为自然对数的底数).根据市场调查,当每公斤卤鸭子的出售价为![]() 元时,日销售量为
元时,日销售量为![]() 公斤.
公斤.
(1)求该商家的每日利润![]() 元与每公斤卤鸭子的出售价
元与每公斤卤鸭子的出售价![]() 元的函数关系式;
元的函数关系式;
(2)若![]() ,当每公斤卤鸭子的出售价
,当每公斤卤鸭子的出售价![]() 为多少元时,该商家的利润
为多少元时,该商家的利润![]() 最大,并求出利润的最大值.
最大,并求出利润的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《孙子算经》中有如下问题:“今有三女,长女五日一归,中女四日一归,少女三日一归.问:三女何日相会?”意思是:“一家出嫁的三个女儿中,大女儿每五天回一次娘家,二女儿每四天回一次娘家,小女儿每三天回一次娘家.三个女儿从娘家同一天走后,至少再隔多少天三人再次相会?”假如回娘家当天均回夫家,若当地风俗正月初二都要回娘家,则从正月初三算起的一百天内,有女儿回娘家的天数有( )
A.58B.59C.60D.61
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com