
【题目】在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为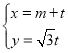 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和C的直角坐标方程;
的普通方程和C的直角坐标方程;
(2)直线![]() 上的点
上的点![]() 为曲线
为曲线![]() 内的点,且直线
内的点,且直线![]() 与曲线
与曲线![]() 交于
交于![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,关于函数
,关于函数![]() 有下列结论:
有下列结论:
①![]() ,
,![]() ;
;
②函数![]() 的图象是中心对称图形,且对称中心是
的图象是中心对称图形,且对称中心是![]() ;
;
③若![]() 是
是![]() 的极大值点,则
的极大值点,则![]() 在区间
在区间![]() 单调递减;
单调递减;
④若![]() 是
是![]() 的极小值点,且
的极小值点,且![]() ,则
,则![]() 有且仅有一个零点.
有且仅有一个零点.
其中正确的结论有________(填写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() (其中
(其中![]() ),证明:
),证明:![]() ;
;
(3)是否存在实数a,使得![]() 在区间
在区间![]() 内恒成立,且关于x的方程
内恒成立,且关于x的方程![]() 在
在![]() 内有唯一解?请说明理由.
内有唯一解?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数![]() 的反函数.定义:若对给定的实数
的反函数.定义:若对给定的实数![]() ,函数
,函数![]() 与
与![]() 互为反函数,则称
互为反函数,则称![]() 满足“
满足“![]() 和性质”;若函数
和性质”;若函数![]() 与
与![]() 互为反函数,则称
互为反函数,则称![]() 满足“
满足“![]() 积性质”.
积性质”.
(1) 判断函数![]() 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由;
(2) 求所有满足“2和性质”的一次函数;
(3) 设函数![]() 对任何
对任何![]() ,满足“
,满足“![]() 积性质”.求
积性质”.求![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四面体P﹣ABC中,PA![]() ,PB=PC=AB=AC=2,BC=2
,PB=PC=AB=AC=2,BC=2![]() ,动点Q在△ABC的内部(含边界),设∠PAQ=α,二面角P﹣BC﹣A的平面角的大小为β,△APQ和△BCQ的面积分别为S1和S2,且满足
,动点Q在△ABC的内部(含边界),设∠PAQ=α,二面角P﹣BC﹣A的平面角的大小为β,△APQ和△BCQ的面积分别为S1和S2,且满足![]() ,则S2的最大值为_____.
,则S2的最大值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是从2020年2月14日至2020年4月19日共66天的新冠肺炎中国/海外新增确诊趋势图,根据该图,下列结论中错误的是( )
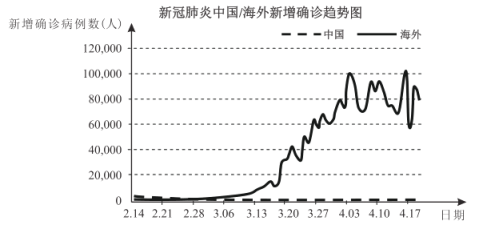
A.从2020年2月14日起中国已经基本控制住国内的新冠肺炎疫情
B.从2020年3月13日至2020年4月3日海外新冠肺炎疫情快速恶化
C.这66天海外每天新增新冠肺炎确诊病例数的中位数在区间![]() 内
内
D.海外新增新冠肺炎确诊病例数最多的一天突破10万例
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为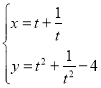 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的普通方程;
的普通方程;
(2)以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,(
,(![]() ),直线
),直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求线段
两点,求线段![]() 的长度
的长度![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是![]() 的中点.
的中点.

(1)设P是![]() 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com