
【题目】已知f(x)=x2+(lga+2)x+lgb,f(-1)=-2,当x∈R时f(x)≥2x恒成立,求实数a的值,并求此时f(x)的最小值?
科目:高中数学 来源: 题型:
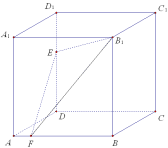
【题目】如图,正方体![]() 中,
中,![]() ,
,![]() 分别为 棱
分别为 棱![]() ,
,![]() 上的点. 已知下列判断:
上的点. 已知下列判断:
①![]() 平面
平面![]() ;②
;②![]() 在侧面
在侧面![]() 上 的正投影是面积为定值的三角形;③在平面
上 的正投影是面积为定值的三角形;③在平面![]() 内总存在与平面
内总存在与平面![]() 平行的直线;④平 面
平行的直线;④平 面![]() 与平面
与平面![]() 所成的二面角(锐角)的大小与点
所成的二面角(锐角)的大小与点![]() 的位置有关,与点
的位置有关,与点![]() 的位置无关.
的位置无关.
其中正确判断的个数有
(A)1个 (B)2个 (C)3个 (D)4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn为等差数列{an}的前n项和,S6=51,a5=13.
(1)求数列{an}的通项公式;
(2)数列{bn}的通项公式是bn=![]() , 求数列{bn}的前n项和Sn .
, 求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日是第二十七届“世界水日”,
日是第二十七届“世界水日”,![]() 月
月![]() 日是第三十二届“中国水周”.我国纪念
日是第三十二届“中国水周”.我国纪念![]() 年“世界水日”和“中国水周”活动的宣传主题为“坚持节水优先,强化水资源管理”.某中学课题小组抽取
年“世界水日”和“中国水周”活动的宣传主题为“坚持节水优先,强化水资源管理”.某中学课题小组抽取![]() 、
、![]() 两个小区各
两个小区各![]() 户家庭,记录他们
户家庭,记录他们![]() 月份的用水量(单位:
月份的用水量(单位:![]() )如下表:
)如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据两组数据完成下面的茎叶图,从茎叶图看,哪个小区居民节水意识更好?
|
| |
| ||
| ||
| ||
|
(2)从用水量不少于![]() 的家庭中,
的家庭中,![]() 、
、![]() 两个小区各随机抽取一户,求
两个小区各随机抽取一户,求![]() 小区家庭的用水量低于
小区家庭的用水量低于![]() 小区的概率.
小区的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某三棱锥的三视图如图所示,图中的3个直角三角形的直角边长度已经标出,则在该三棱锥中,最短的棱和最长的棱所在直线的成角余弦值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com