解:(1)f(x)=

sin2x-cos
2x-

=

sin2x-
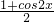
-

=

sin2x-

cos2x-1=sin(2x-

)-1,
∵-1≤sin(2x-

)-≤1,
∴f(x)的最小值为-2,
又ω=2,
则最小正周期是T=

=π;
(2)由f(C)=sin(2C-

)-1=0,得到sin(2C-

)=1,
∵0<C<π,∴-

<2C-

<

,
∴2C-

=

,即C=

,
∵sinB=2sinA,∴由正弦定理得b=2a①,又c=

,
∴由余弦定理,得c
2=a
2+b
2-2abcos

,即a
2+b
2-ab=3②,
联立①②解得:a=1,b=2.
分析:(1)将f(x)解析式第二项利用二倍角的余弦函数公式化简,整理后再利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,由正弦函数的值域得出f(x)的最小值,找出ω的值,代入周期公式,即可求出f(x)的最小正周期;
(2)由(1)确定的f(x)解析式及f(C)=0,求出sin(2C-

)=1,由C的范围,求出2x-

的范围,利用特殊角的三角函数值及正弦函数的图象求出C的度数,由sinB=2sinA,利用正弦定理得到b=2a①,再利用余弦定理得到c
2=a
2+b
2-2abcosC,将c与cosC的值代入得到关于a与b的方程,记作②,联立①②即可求出a与b的值.
点评:此题属于解三角形的题型,涉及的知识有:正弦、余弦定理,正弦函数的定义域与值域,二倍角的余弦函数公式,以及两角和与差的正弦函数公式,熟练掌握定理及公式是解本题的关键.

 sin2x-cos2x-
sin2x-cos2x- ,x∈R.
,x∈R. ,f(C)=0,若sinB=2sinA,求a,b的值.
,f(C)=0,若sinB=2sinA,求a,b的值. sin2x-cos2x-
sin2x-cos2x-
 sin2x-
sin2x-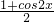 -
-
 sin2x-
sin2x- cos2x-1=sin(2x-
cos2x-1=sin(2x- )-1,
)-1, )-≤1,
)-≤1, =π;
=π; )-1=0,得到sin(2C-
)-1=0,得到sin(2C- )=1,
)=1, <2C-
<2C- <
< ,
, =
= ,即C=
,即C= ,
, ,
, ,即a2+b2-ab=3②,
,即a2+b2-ab=3②, )=1,由C的范围,求出2x-
)=1,由C的范围,求出2x- 的范围,利用特殊角的三角函数值及正弦函数的图象求出C的度数,由sinB=2sinA,利用正弦定理得到b=2a①,再利用余弦定理得到c2=a2+b2-2abcosC,将c与cosC的值代入得到关于a与b的方程,记作②,联立①②即可求出a与b的值.
的范围,利用特殊角的三角函数值及正弦函数的图象求出C的度数,由sinB=2sinA,利用正弦定理得到b=2a①,再利用余弦定理得到c2=a2+b2-2abcosC,将c与cosC的值代入得到关于a与b的方程,记作②,联立①②即可求出a与b的值.

