证明:(1)证明:令x=y=0,则f(0)=f(0)+f(0),从而f(0)=0,
令y=-x,则f(0)=f(x)+f(-x)=0,
从而f(-x)=-f(x),即f(x)是奇函数.…(4分)
(2)设x
1,x
2∈R,且x
1<x
2,则x
1-x
2<0,从而f(x
1-x
2)<0,
又f(x
1-x
2)=f[x
1+(-x
2)]=f(x
1)+f(-x
2)=f(x
1)-f(x
2).
∴f(x
1)-f(x
2)<0,即f(x
1)<f(x
2).
∴函数f(x)为R上的增函数,
∴当x∈[-4,4]时,f(x)必为增函数.
又由f(-1)=-2,得-f(1)=-2,
∴f(1)=2,
∴当x=-4时,f(x)
min=f(-4)=-f(4)=-4f(1)=-8;
当x=4时,f(x)
max=f(4)=4f(1)=8. …(9分)
(3)由已知得

.
∴
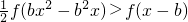
.
∴f(bx
2-b
2x)>2f(x-b),即f(bx
2-b
2x)>f(2x-2b).
∵f(x)为R上增函数,
∴bx
2-b
2x>2x-2b,
∴bx
2-(b
2+2)x+2b>0,即(bx-2)(x-b)>0.
当b=0时,-2x>0,
∴不等式的解集为{x|x<0}.
当b<0时,(-bx+2)(x-b)<0.
1°当
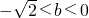
时,不等式的解集为
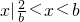
,
2°当b<

时,不等式的解集为
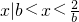
,
3°当b=

时,不等式的解集为∅.
分析:(1)令x=y=0?f(0)=0,再令y=-x,?f(-x)=-f(x);
(2)设x
1,x
2∈R,且x
1<x
2,结合条件用单调性的定义证明函数f(x)为R上的增函数,从而当x∈[-4,4]时,f(x)亦为增函数;又由f(-1)=-2,得-f(1)=-2,?f(1)=2,从而当x=-4时,求得f(x)
min=f(-4)=-f(4)=-8;当x=4时,f(x)
max=f(4)=8;
(3)由
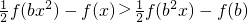
(b≤0)?f(bx
2-b
2x)>f(2x-2b)结合单调递增性?bx
2-b
2x>2x-2b.再对b
2的系数b分b=0与b≠0讨论,解得其解集即可.
点评:本题考查抽象函数及其应用,着重考查赋值法判断函数奇偶性,用定义法(单调性定义)证明函数单调性,转化思想与分类讨论思想求不等式的解集,逻辑复杂,综合性强,属于难题.

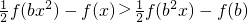 (b≤0).
(b≤0). .
.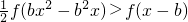 .
.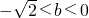 时,不等式的解集为
时,不等式的解集为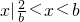 ,
, 时,不等式的解集为
时,不等式的解集为 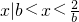 ,
, 时,不等式的解集为∅.
时,不等式的解集为∅.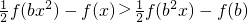 (b≤0)?f(bx2-b2x)>f(2x-2b)结合单调递增性?bx2-b2x>2x-2b.再对b2的系数b分b=0与b≠0讨论,解得其解集即可.
(b≤0)?f(bx2-b2x)>f(2x-2b)结合单调递增性?bx2-b2x>2x-2b.再对b2的系数b分b=0与b≠0讨论,解得其解集即可.
