
【题目】下列说法正确的是( )
A.“sinα= ![]() ”是“cos2α=
”是“cos2α= ![]() ”的必要不充分条件
”的必要不充分条件
B.已知命题p:?x∈R,使2x>3x;命题q:?x∈(0,+∞),都有 ![]() <
< ![]() ,则p∧(¬q)是真命题
,则p∧(¬q)是真命题
C.命题“若xy=0,则x=0或y=0”的否命题是“若xy≠0,则x≠0或y≠0”
D.从匀速传递的生产流水线上,质检员每隔5分钟从中抽取一件产品进行某项指标检测,这是分成抽样
【答案】B
【解析】解:由cos2α= ![]() ,得
,得 ![]() ,解得sinα=
,解得sinα= ![]() ,∴“sinα=
,∴“sinα= ![]() ”是“cos2α=
”是“cos2α= ![]() ”的充分不必要条件,故A错误; 命题p:x∈R,使2x>3x为真命题,命题q:x∈(0,+∞),都有
”的充分不必要条件,故A错误; 命题p:x∈R,使2x>3x为真命题,命题q:x∈(0,+∞),都有 ![]() <
< ![]() 为假命题,则p∧(¬q)是真命题,故B正确;
为假命题,则p∧(¬q)是真命题,故B正确;
命题“若xy=0,则x=0或y=0”的否命题是“若xy≠0,则x≠0且y≠0”,故C错误;
从匀速传递的生产流水线上,质检员每隔5分钟从中抽取一件产品进行某项指标检测,这是系统抽样,故D错误.
故选:B.
【考点精析】根据题目的已知条件,利用命题的真假判断与应用的相关知识可以得到问题的答案,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】执行如图的程序框图,当n≥2,n∈Z时,fn(x)表示fn﹣1(x)的导函数,若输入函数f1(x)=sinx﹣cosx,则输出的函数fn(x)可化为( ) 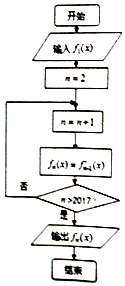
A.![]() sin(x+
sin(x+ ![]() )
)
B.![]() sin(x﹣
sin(x﹣ ![]() )??
)??
C.﹣ ![]() sin(x+
sin(x+ ![]() )
)
D.﹣ ![]() sin(x﹣
sin(x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若以直角坐标系xOy的O为极点,Ox为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程是ρ= ![]() .
.
(1)将曲线C的极坐标方程化为直角坐标方程,并指出曲线是什么曲线;
(2)若直线l的参数方程为 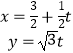 (t为参数)当直线l与曲线C相交于A,B两点,求|
(t为参数)当直线l与曲线C相交于A,B两点,求| ![]() |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
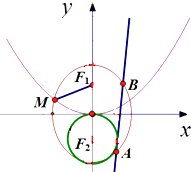
【题目】已知F1 , F2分别为椭圆C1: ![]() (a>b>0)的上下焦点,其F1是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=
(a>b>0)的上下焦点,其F1是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|= ![]() .
. 
(1)试求椭圆C1的方程;
(2)与圆x2+(y+1)2=1相切的直线l:y=k(x+t)(t≠0)交椭圆于A,B两点,若椭圆上一点P满足 ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com