一个四边形的四个内角成等差数列,最小角为40°,则最大角为 .
【答案】
分析:设出等差数列的公差为d,由最小角的度数,利用等差数列的通项公式分别表示出其他三个角,然后利用四边形的内角和为360°列出关于d的方程,求出方程的解得到d的值,即可求出最大角的度数.
解答:解:∵四边形的四个内角成等差数列,最小角为40°,
∴设等差数列的公差为d,则其他内角为40°+d,40°+2d,40°+3d,
根据四边形的内角和列方程得:
40°+(40°+d)+(40°+2d)+(40°+3d)=360°,
解得:d=

°,
则最大角为40°+3d=40°+3×
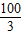
°=140°.
故答案为:140°
点评:此题考查了等差数列的性质,等差数列的通项公式,以及四边形的内角和,熟练掌握等差数列的通项公式及性质是解本题的关键.

 °,
°,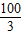 °=140°.
°=140°.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案