
【题目】如图,在平面直角坐标系xOy中,设椭圆 ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.
=1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.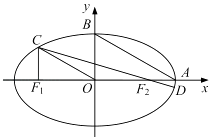
(1)若OC∥AB,求e的值;
(2)连结CF2并延长交椭圆于另一点D若 ![]() ≤e≤
≤e≤ ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)
解:椭圆 ![]() =1(a>b>0)的焦距为2c,
=1(a>b>0)的焦距为2c,
由CF1⊥x轴.则C(﹣c,y0),y0>0,
由C在椭圆上,则y0= ![]() ,则C(﹣c,
,则C(﹣c, ![]() ),
),
由OC∥AB,则﹣ ![]() =kOC=kAB=﹣
=kOC=kAB=﹣ ![]() ,则b=c,
,则b=c,
e= ![]() =
= ![]() =
= ![]() ,
,
e的值 ![]()
(2)
解:设D(x1,y1),设 ![]() =λ
=λ ![]() ,
,
C(﹣c, ![]() ),F2(c,0),
),F2(c,0),
故 ![]() =(2c,﹣
=(2c,﹣ ![]() ),
), ![]() =(x1﹣c,y1),
=(x1﹣c,y1),
由 ![]() =λ
=λ ![]() ,则2c=λ(x1﹣c),﹣
,则2c=λ(x1﹣c),﹣ ![]() =λy1,则D(
=λy1,则D( ![]() c,﹣
c,﹣ ![]() ),
),
由点D在椭圆上,则( ![]() )2e2+
)2e2+ ![]() =1,整理得:(λ2+4λ+3)e2=λ2﹣1,
=1,整理得:(λ2+4λ+3)e2=λ2﹣1,
由λ>0,e2= ![]() =
= ![]() =1﹣
=1﹣ ![]() ,
,
由 ![]() ≤e≤
≤e≤ ![]() ,则
,则 ![]() ≤e2≤
≤e2≤ ![]() ,则
,则 ![]() ≤1﹣
≤1﹣ ![]() ≤
≤ ![]() ,
,
解得: ![]() ≤λ≤5,
≤λ≤5,
∴ ![]() 的取值范围[
的取值范围[ ![]() ,5]
,5]
【解析】(1)由CF1⊥x轴.则C(﹣c, ![]() ),根据直线的斜率相等,即可求得b=c,利用离心率公式即可求得e的值;(2)根据向量的坐标运算,求得D点坐标,代入椭圆方程,求得e2=
),根据直线的斜率相等,即可求得b=c,利用离心率公式即可求得e的值;(2)根据向量的坐标运算,求得D点坐标,代入椭圆方程,求得e2= ![]() =1﹣
=1﹣ ![]() ,由离心率的取值范围,即可求得λ的取值范围.
,由离心率的取值范围,即可求得λ的取值范围.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】某手机厂商推出一次智能手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
频数 | 20 | 40 | 80 | 50 | 10 | |
男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
频数 | 45 | 75 | 90 | 60 | 30 |
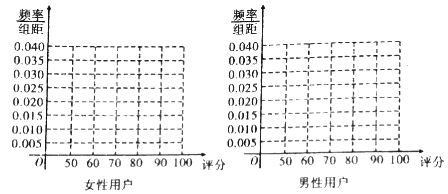
(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的方差大小(不计算具体值,给出结论即可);
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取3名用户,求3名用户评分小于90分的人数的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中社团进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”,通过调查分别得到如图所示统计表和各年龄段人数频率分布直方图: 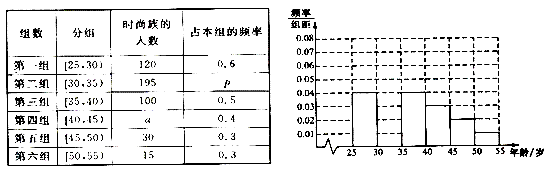
完成以下问题:
(Ⅰ)补全频率分布直方图并求n , a , p的值;
(Ⅱ)从[40,50)岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络时尚达人大赛,其中选取3人作为领队,记选取的3名领队中年龄在[40,45)岁的人数为X,求X的分布列和期望E(X)..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xe2x﹣lnx﹣ax.
(1)当a=0时,求函数f(x)在[ ![]() ,1]上的最小值;
,1]上的最小值;
(2)若x>0,不等式f(x)≥1恒成立,求a的取值范围;
(3)若x>0,不等式f( ![]() )﹣1≥
)﹣1≥ ![]() e
e ![]() +
+ ![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在考试测评中,常用难度曲线图来检测题目的质量,一般来说,全卷得分高的学生,在某道题目上的答对率也应较高,如果是某次数学测试压轴题的第1、2问得分难度曲线图,第1、2问满分均为6分,图中横坐标为分数段,纵坐标为该分数段的全体考生在第1、2问的平均难度,则下列说法正确的是( ) 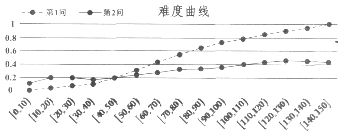
A.此题没有考生得12分
B.此题第1问比第2问更能区分学生数学成绩的好与坏
C.分数在[40,50)的考生此大题的平均得分大约为4.8分
D.全体考生第1问的得分标准差小于第2问的得分标准差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com