
【题目】(1)双曲线![]() 的离心率为_____________
的离心率为_____________
(2)点P是椭圆![]() 上一点,
上一点,![]() 分别是椭圆的左、右焦点,若
分别是椭圆的左、右焦点,若![]() ,则
,则![]() 的大小______ .
的大小______ .
(3)如果![]() 是抛物线y2=4x上的点,它们的横坐标依次为
是抛物线y2=4x上的点,它们的横坐标依次为![]() ,F是抛物线的焦点,若
,F是抛物线的焦点,若![]() 则
则![]() _______________.
_______________.
(4)若x,y满足约束条件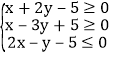 ,则z=x2+y2的最大值为______________.
,则z=x2+y2的最大值为______________.
【答案】![]()
![]()
![]() 25
25
【解析】
(1)由双曲线的a和c,利用离心率公式求解即可;
(2)设|PF1|=m,|PF2|=n,由椭圆的定义及题干条件可得m+n和mn,再利用余弦定理求角即可;
(3)由抛物线的焦半径定义可知|P1F|+|P2F|+…|P8F|=(x1+1)+(x2+1)+…+(x8+1),代入条件即可得解;
(4)根据不等式组画出可行域,再由x2+y2是点(x,y)到原点的距离的平方,数形结合求解即可.
(1)由双曲线![]() 得
得![]() ,
,
所以离心率![]() ,故答案为
,故答案为![]() .
.
(2)椭圆![]() ,
,
可得2a=8,设|PF1|=m,|PF2|=n,可得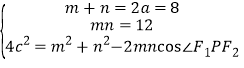 ,
,
化简可得:∴∠F1PF2=60°,故答案为60°.
(3)∵抛物线y2=4x的焦点为F(1,0),准线为x=-1,
∴根据抛物线的定义,Pi(i=1,2,3,…,8)到焦点的距离等于Pi到准线的距离,即|PiF|=xi+1,
可得|P1F|+|P2F|+…|P8F|=(x1+1)+(x2+1)+…+(x8+1)
=(x1+x2+…+x8)+8,
∵x1+x2+…+x8=10,∴|P1F|+|P2F|+…|P8F|=10+8=18.
故答案为18.
(4)如图,作出可行域,
x2+y2是点(x,y)到原点的距离的平方,
故最大值为点A(4,3)到原点的距离的平方,即|AO|2=25,故答案为25.


科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2. 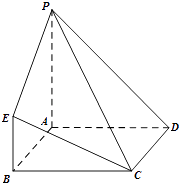
(1)求证:CE∥平面PAD;
(2)求PD与平面PCE所成角的正弦值;
(3)在棱AB上是否存在一点F,使得平面DEF⊥平面PCE?如果存在,求 ![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( ) 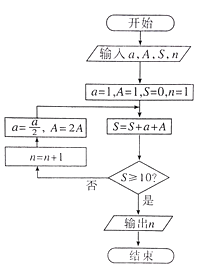
A.4
B.5
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆: ![]() (a>b>0),左右焦点分别是F1 , F2 , 焦距为2c,若直线
(a>b>0),左右焦点分别是F1 , F2 , 焦距为2c,若直线 ![]() 与椭圆交于M点,满足∠MF1F2=2∠MF2F1 , 则离心率是( )
与椭圆交于M点,满足∠MF1F2=2∠MF2F1 , 则离心率是( )
A.![]()
B.![]() -1
-1
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着苹果6手机的上市,很多消费者觉得价格偏高,尤其是一部分大学生可望而不可及,因此“国美在线”推出无抵押分期付款购买方式,某分期店对最近100位采用分期付款的购买者进行统计,统计结果如下表所示:
付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
频 数 | 35 | 25 | a | 10 | b |
已知分3期付款的频率为0.15,并且店销售一部苹果6,顾客分1期付款,其利润为1千元;分2期或3期付款,其利润为1.5千元;分4期或5期付款,其利润为2千元,以频率作为概率.
(1)求事件A:“购买的3位顾客中,至多有1位分4期付款”的概率;
(2)用X表示销售一该手机的利润,求X的分布列及数学期望E(x)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为![]() .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为![]() 时,求k的值.
时,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M的方程为x2+(y﹣2)2=1,直线l的方程为x﹣2y=0,点P在直线l上,过点P作圆M的切线PA,PB,切点为A,B.
(1)若点P的横坐标为1,求切线PA,PB的方程;
(2)若点P的纵坐标为a,且在圆M上存在点Q到点P的距离为1,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com