
【题目】已知椭圆C1: ![]() =1(a>b>0)的左、右焦点分别为F1、F2 , 其中F2也是抛物线C2:y2=4x的焦点,M是C1与C2在第一象限的交点,且
=1(a>b>0)的左、右焦点分别为F1、F2 , 其中F2也是抛物线C2:y2=4x的焦点,M是C1与C2在第一象限的交点,且 ![]()
(I)求椭圆C1的方程;
(Ⅱ)已知菱形ABCD的顶点A、C在椭圆C1上,顶点B、D在直线7x﹣7y+1=0上,求直线AC的方程.
【答案】解:(I)设点M为(x1 , y1),∵F2是抛物线y2=4x的焦点,
∴F2(1,0);
又|MF2|= ![]() ,由抛物线定义知
,由抛物线定义知
x1+1= ![]() ,即x1=
,即x1= ![]() ;
;
由M是C1与C2的交点,
∴y12=4x1 , 即y1=± ![]() ,这里取y1=
,这里取y1= ![]() ;
;
又点M( ![]() ,
, ![]() )在C1上,
)在C1上,
∴ ![]() +
+ ![]() =1,且b2=a2﹣1,
=1,且b2=a2﹣1,
∴9a4﹣37a2+4=0,∴ ![]() (舍去),
(舍去),
∴a2=4,b2=3;
∴椭圆C1的方程为: ![]()
(II)∵直线BD的方程为:7x﹣7y+1=0,在菱形ABCD中,AC⊥BD,
不妨设直线AC的方程为x+y=m,
则 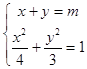
∴消去y,得7x2﹣8mx+4m2﹣12=0;
∵点A、C在椭圆C1上,
∴(﹣8m)2﹣4×7×(4m2﹣12)>0,即m2<7,∴﹣ ![]() <m<
<m< ![]() ;
;
设A(x1 , y1),C(x2 , y2),
则x1+x2= ![]() ,y1+y2=(﹣x1+m)+(﹣x2+m)=﹣(x1+x2)+2m=﹣
,y1+y2=(﹣x1+m)+(﹣x2+m)=﹣(x1+x2)+2m=﹣ ![]() +2m=
+2m= ![]() ,
,
∴AC的中点坐标为 ![]() ,
,
由菱形ABCD知,点 ![]() 也在直线BD:7x﹣7y+1=0上,
也在直线BD:7x﹣7y+1=0上,
即7× ![]() ﹣7×
﹣7× ![]() +1=0,∴m=﹣1,由m=﹣1∈
+1=0,∴m=﹣1,由m=﹣1∈ ![]() 知:
知:
直线AC的方程为:x+y=﹣1,即x+y+1=0
【解析】(Ⅰ)设点M为(x1 , y1),由F2是抛物线y2=4x的焦点,知F2(1,0);|MF2|= ![]() ,由抛物线定义知x1+1=
,由抛物线定义知x1+1= ![]() ,即x1=
,即x1= ![]() ;由M是C1与C2的交点,y12=4x1 , 由此能求出椭圆C1的方程.(Ⅱ)直线BD的方程为:7x﹣7y+1=0,在菱形ABCD中,AC⊥BD,设直线AC的方程为x+y=m,由
;由M是C1与C2的交点,y12=4x1 , 由此能求出椭圆C1的方程.(Ⅱ)直线BD的方程为:7x﹣7y+1=0,在菱形ABCD中,AC⊥BD,设直线AC的方程为x+y=m,由 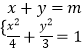 ,得7x2﹣8mx+4m2﹣12=0.由点A、C在椭圆C1上,知(﹣8m)2﹣4×7×(4m2﹣12)>0,由此能导出直线AC的方程.
,得7x2﹣8mx+4m2﹣12=0.由点A、C在椭圆C1上,知(﹣8m)2﹣4×7×(4m2﹣12)>0,由此能导出直线AC的方程.


科目:高中数学 来源: 题型:
【题目】在淘宝网上,某店铺专卖孝感某种特产.由以往的经验表明,不考虑其他因素,该特产每日的销售量y(单位:千克)与销售价格x(单位:元/千克,1<x≤5)满足:当1<x≤3时,y=a(x﹣3)2+ ![]() ,(a,b为常数);当3<x≤5时,y=﹣70x+490.已知当销售价格为2元/千克时,每日可售出该特产600千克;当销售价格为3元/千克时,每日可售出150千克.
,(a,b为常数);当3<x≤5时,y=﹣70x+490.已知当销售价格为2元/千克时,每日可售出该特产600千克;当销售价格为3元/千克时,每日可售出150千克.
(1)求a,b的值,并确定y关于x的函数解析式;
(2)若该特产的销售成本为1元/千克,试确定销售价格x的值,使店铺每日销售该特产所获利润f(x)最大(x精确到0.1元/千克).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,三边a,b,c所对应的角分别是A,B,C,已知a,b,c成等比数列.
(1)若 ![]() +
+ ![]() =
= ![]() ,求角B的值;
,求角B的值;
(2)若△ABC外接圆的面积为4π,求△ABC面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,b>0,函数f(x)=|x+a|+|2x﹣b|的最小值为1.
(1)求证:2a+b=2;
(2)若a+2b≥tab恒成立,求实数t的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com