
【题目】某赛季甲、乙两位运动员每场比赛得分的茎叶图如图所示.
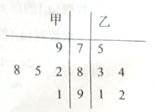
(1)从甲、乙两人的这5次成绩中各随机抽取一个,求甲的成绩比乙的成绩高的概率;
(2)试用统计学中的平均数、方差知识对甲、乙两位运动员的测试成绩进行分析.
【答案】(1)![]() ;(2) 甲、乙两位运动员平均水平相当,甲运动员比乙运动员发挥稳定.
;(2) 甲、乙两位运动员平均水平相当,甲运动员比乙运动员发挥稳定.
【解析】
试题
(1)列出所有可能的事件,结合古典概型计算公式可得甲的成绩比乙的成绩高的概率是![]() ;
;
(2)甲乙两人平均数相等,甲的方差较小,则甲、乙两位运动员平均水平相当,甲运动员比乙运动员发挥稳定.
试题解析:
(1)记甲被抽到的成绩为x,乙被抽到成绩为y,用数对(x,y)表示基本事件,
则从甲、乙两人的这5次成绩中各随机抽取一个,共包含以下基本事件:
(79,75),(79,83),(79,84),(79,91),(79,92),
(82,75),(82,83),(82,84),(82,91),(82,92),
(85,75),(85,83),(85,84),(85,91),(85,92),
(88,75),(88,83),(88,84),(88,91),(88,92),
(91,75),(91,83),(91,84),(91,91),(91,92),
基本事件总数n=25,
设“甲的成绩比乙的成绩高”为事件A,则事件A包含以下基本事件:
(79,75),(82,75),(85,75),(85,83),(85,84),
(88,75),(88,83),(88,84),(91,75),(91,83),(91,84),
事件A包含的基本事件数m=11,
所以P(A)=![]() =
=![]() .
.
(2)![]() 甲=
甲=![]() (79+82+85+88+91)=85;
(79+82+85+88+91)=85;
乙=![]() (75+83+84+91+92)=85
(75+83+84+91+92)=85
甲得分的方差
s=![]() [(79-85)2+(82-85)2+(85-85)2+(88-85)2+(91-85)2)]=18;
[(79-85)2+(82-85)2+(85-85)2+(88-85)2+(91-85)2)]=18;
乙得分的方差
s=![]() [(75-85)2+(83-85)2+(84-85)2+(91-85)2+(92-85)2)]=38.
[(75-85)2+(83-85)2+(84-85)2+(91-85)2+(92-85)2)]=38.
从计算结果看,![]() 甲=
甲=![]() 乙,s<s,所以甲、乙两位运动员平均水平相当,甲运动员比乙运动员发挥稳定.
乙,s<s,所以甲、乙两位运动员平均水平相当,甲运动员比乙运动员发挥稳定.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为抛物线
为抛物线![]() 上异于原点的任意一点,过点
上异于原点的任意一点,过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于另一点
于另一点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,且有
,且有![]() .当点
.当点![]() 的横坐标为3时,
的横坐标为3时,![]()
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)若直线![]() ,且
,且![]() 和抛物线
和抛物线![]() 有且只有一个公共点
有且只有一个公共点![]() ,试问直线
,试问直线![]() (
(![]() 为抛物线
为抛物线![]() 上异于原点的任意一点)是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
上异于原点的任意一点)是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是自然对数的底数,函数
是自然对数的底数,函数![]() 与
与![]() 的定义域都是
的定义域都是![]() .
.
(1)求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)判断函数![]() 零点个数;
零点个数;
(3)用![]() 表示
表示![]() 的最小值,设
的最小值,设![]() ,
,![]() ,若函数
,若函数![]() 在
在![]() 上为增函数,求实数
上为增函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() ,
,![]() .
.
(1)若集合![]() 含有三个元素,且
含有三个元素,且![]() ,这样的集合
,这样的集合![]() 有多少个?所有集合
有多少个?所有集合![]() 中个元素之和是多少?
中个元素之和是多少?
(2)若集合![]() 各含有三个元素,且
各含有三个元素,且![]() ,
,![]() ,
,![]() ,这样的集合
,这样的集合![]() 有多少种配对方式?
有多少种配对方式?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 、
、![]() 满足
满足![]() (
(![]() N*),则称
N*),则称![]() 为数列
为数列![]() 的“偏差数列”.
的“偏差数列”.
(1)若![]() 为常数列,且为
为常数列,且为![]() 的“偏差数列”,试判断
的“偏差数列”,试判断![]() 是否一定为等差数列,并说明理由;
是否一定为等差数列,并说明理由;
(2)若无穷数列![]() 是各项均为正整数的等比数列,且
是各项均为正整数的等比数列,且![]() ,
,![]() 为数列
为数列![]() 的“偏差数列”,求
的“偏差数列”,求![]() 的值;
的值;
(3)设![]() ,
,![]() 为数列
为数列![]() 的“偏差数列”,
的“偏差数列”,![]() ,
,![]() 且
且![]() ,若
,若![]() 对任意
对任意![]() 恒成立,求实数M的最小值.
恒成立,求实数M的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,长轴是短轴的
,长轴是短轴的![]() 倍,且椭圆
倍,且椭圆![]() 过点
过点![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 过点
过点![]() ,坐标平面上的点
,坐标平面上的点![]() 满足到直线
满足到直线![]() 的距离为定值
的距离为定值![]() .
.
(1)写出椭圆![]() 方程;
方程;
(2)若椭圆![]() 上恰好存在
上恰好存在![]() 个这样的点
个这样的点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设min{m,n}表示m,n二者中较小的一个,已知函数f(x)=x2+8x+14,g(x)=![]() (x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,则a的最大值为
(x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,则a的最大值为
A.-4B.-3C.-2D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com