
【题目】某工厂今年1月、2月、3月生产某种产品的数量分别是1万件、2万件、1.3万件,为了预测以后每个月的产量,以这三个月的产品数量为依据,用一个函数模拟该产品的月产量y与月份x的关系,模拟函数可以选用二次函数或函数y=abx+c(其中a,b,c为常数),已知4月份该产品的产量为1.37万件,请问用以上哪个函数作为模拟函数较好?并说明理由.
【答案】选用y=-0.8×0.5x+1.4作为模拟函数较好.
【解析】试题分析:由题意分别列示求出两种函数模型的待求系数,然后分别取x=4求出相应的函数值,比较大小得答案.
试题解析:
根据题意,该产品的月产量y是月份x的函数,可供选用的函数有两种,其中哪一种函数确定的4月份该产品的产量越接近于1.37万件,哪种函数作为模拟函数就较好,故应先确定这两个函数的具体解析式.
设y1=f(x)=px2+qx+r(p,q,r为常数,
且p≠0),y2=g(x)=abx+c,根据已知有
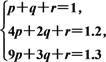 和
和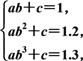
解得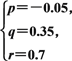 和
和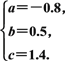
所以f(x)=-0.05x2+0.35x+0.7,g(x)=-0.8×0.5x+1.4.所以f(4)=1.3,g(4)=1.35.
显然g(4)更接近于1.37,故选用y=-0.8×0.5x+1.4作为模拟函数较好.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
【题目】某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
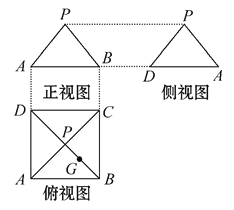
(1)根据三视图,画出该几何体的直观图.
(2)在直观图中,①证明:PD∥平面AGC;
②证明:平面PBD⊥平面AGC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品上市30天内每件的销售价格![]() 元与时间
元与时间![]() 天函数关系是
天函数关系是
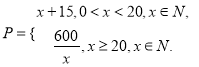 该商品的日销售量
该商品的日销售量![]() 件与时间
件与时间![]() 天函数关系是
天函数关系是
![]() .(1)求该商品上市第20天的日销售金额;
.(1)求该商品上市第20天的日销售金额;
(2)求这个商品的日销售金额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为常数,
为常数,![]() ).(Ⅰ)求函数
).(Ⅰ)求函数![]() 的单调区间;(Ⅱ)当
的单调区间;(Ⅱ)当![]() 时,是否存在实数
时,是否存在实数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 恒成立?如果存在,求
恒成立?如果存在,求![]() 的取值范围;如果不存在,请说明理由(其中
的取值范围;如果不存在,请说明理由(其中![]() 是自然对数的底数,
是自然对数的底数,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盐化某厂决定采用以下方式对某块盐池进行开采:每天开采的量比上一天减少![]() ,10天后总量变为原来的一半,为了维持生态平衡,剩余总量至少要保留原来的
,10天后总量变为原来的一半,为了维持生态平衡,剩余总量至少要保留原来的![]() ,已知到今天为止,剩余的总量是原来的
,已知到今天为止,剩余的总量是原来的![]() .
.
(1)求![]() 的值;
的值;
(2)到今天为止,工厂已经开采了几天?
(3)今后最多还能再开采多少天?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下的对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求y关于x的线性回归方程。
(3)如果广告费支出为一千万元,预测销售额大约为多少百万元?
参考公式
用最小二乘法求线性回归方程系数公式: ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com