[题目]已知复数z=k﹣2i的共轭复数 .且z﹣( ﹣i)= ﹣2i．(1)求k的值,的直线l的斜率为k.求直线l与曲线y= 以及y轴所围成的图形的面积．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知复数z=k﹣2i（k∈R）的共轭复数，且z﹣（ ﹣i）= ﹣2i．
（1）求k的值；
（2）若过点（0，﹣2）的直线l的斜率为k，求直线l与曲线y= 以及y轴所围成的图形的面积．

【答案】
（1）解：复数z=k﹣2i的共轭复数 =k+2i，

且z﹣（ ﹣i）= ﹣2i，

∴（k﹣2i）﹣（ ﹣i）= （k+2i）﹣2i，

∴（k﹣ ）﹣i= k﹣i，

即k﹣ = k，

解得k=1；

（2）解：过点（0，﹣2）的直线l的斜率为k=1，

∴直线l的方程为：y=x﹣2；

令，解得，

∴直线l与曲线y= 的交点为（4，2）；

如图所示，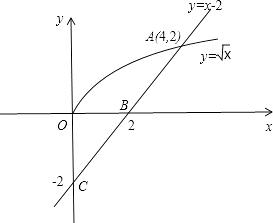

曲线y= 与直线y=x﹣2以及y轴所围成的图形的面积为：

S△OBC+∫02 dx+∫24（ ﹣x+2）dx= ×2×2+ +（ ﹣ x2+2x） = ．

【解析】（1）利用复数相等与代数运算，列出方程求出k的值；（2）写出直线l的方程，求出直线l与曲线y= 的交点，再利用积分求对应的面积．

练习册系列答案

仁爱英语同步阅读与完形填空周周练系列答案

黄冈新思维培优考王单元加期末卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】对于定义域为的函数，如果存在区间（），同时满足：

①在内是单调函数；②当定义域是时，的值域也是．

则称函数是区间上的“保值函数”．

（1）求证：函数不是定义域上的“保值函数”；

（2）已知（）是区间上的“保值函数”，求的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数=ex(ex﹣a)﹣a2x．

（1）讨论的单调性；

（2）若，求a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=ax﹣1（x≥0）的图象经过点（2，），其中a＞0，a≠1．
（1）求a的值；
（2）求函数f（x）=a2x﹣ax﹣2+8，x∈[﹣2，1]的值域．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=﹣ （x∈R），区间M=[a，b]（a＜b），集合N={y|y=f （x），x∈M}．若M=N，则b﹣a的值是

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】己知 a＞0 且 a≠1，若函数f（x）=loga（x﹣1），g（x）=loga（5﹣x）．
（1）求函数h（x）=f（x）﹣g（x）的定义域；
（2）讨论不等式f（x）≥g（x）成立时x的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】对于两个定义域相同的函数f（x）、g（x），若存在实数m，n，使h（x）=mf（x）+ng（x），则称函数f（x）是由“基函数f（x），g（x）”生成的．
（1）若f（x）=x2+3x和g（x）=3x+4生成一个偶函数h（x），求h（2）的值；
（2）若h（x）=2x2+3x﹣1是由f（x）=x2+ax和g（x）=x+b生成，其中a，b∈R且ab≠0，求的取值范围；
（3）利用“基函数f（x）=log4（4x+1），g（x）=x﹣1）”生成一个函数h（x），使得h（x）满足：
①是偶函数，②有最小值1，求h（x）的解析式．