
【题目】如图所示,在正三棱柱ABC﹣A1B1C1中,点D在边BC上,AD⊥C1D. 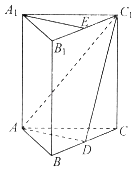
(1)求证:平面ADC1⊥平面BCC1B1;
(2)如果点E是B1C1的中点,求证:AE∥平面ADC1 .
【答案】
(1)证明:∵在正三棱柱ABC﹣A1B1C1中,点D在边BC上,AD⊥C1D,
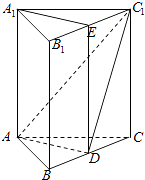
∴CC1⊥平面ABC,又AD平面ABC,∴AD⊥CC1,
又C1D∩CC1=C1,∴AD⊥平面BCC1B1.
AD面ADC1,∴平面ADC1⊥平面BCC1B1
(2)解:∵AD⊥平面BCC1B1,∴AD⊥BC,
∵在正三棱柱ABC﹣A1B1C1中,AB=BC=AC,∴D是BC中点,
连结ED,∵点E是C1B1的中点,
∴AA1∥DE且AA1=DE,∴四边形AA1DE是平行四边形,
∴A1E∥AD,
又A1E面ADC1,AD平面ADC1.
∴A1E∥平面ADC1.
【解析】(1)推导出AD⊥C1D,从而CC1⊥平面ABC,进而AD⊥CC1,由此能证明AD⊥平面BCC1B1.即平面ADC1⊥平面BCC1B1(2)由AD⊥BC,得D是BC中点,连结ED,得四边形AA1DE是平行四边形,由此能证明A1E∥平面ADC1.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直.


科目:高中数学 来源: 题型:
【题目】已知锐角△ABC的三个内角A,B,C的对边分别为a,b,c,且 ![]() =(a,b+c),
=(a,b+c), ![]() .
.
(1)求角A;
(2)若a=3,求△ABC面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图四棱锥E﹣ABCD中,四边形ABCD为平行四边形,△BCE为等边三角形,△ABE是以∠A为直角的等腰直角三角形,且AC=BC. (Ⅰ)证明:平面ABE⊥平面BCE;
(Ⅱ)求二面角A﹣DE﹣C的余弦值.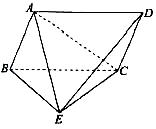
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,C> ![]() ,若函数y=f(x)在[0,1]上为单调递减函数,则下列命题正确的是( )
,若函数y=f(x)在[0,1]上为单调递减函数,则下列命题正确的是( )
A.f(cosA)>f(cosB)
B.f(sinA)>f(sinB)
C.f(sinA)>f(cosB)
D.f(sinA)<f(cosB)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)+B,A>0,ω>0,|φ|< ![]() 在某一个周期的图象时,列表并填入了部分数据,如表:
在某一个周期的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x | x1 |
| x2 |
| x3 |
Asin(ωx+φ)+B | 0 |
| 0 | ﹣ | 0 |
(1)请求出上表中的x1 , x2 , x3 , 并直接写出函数f(x)的解析式;
(2)若3sin2 ![]() ﹣
﹣ ![]() mf(
mf( ![]() ﹣
﹣ ![]() )≥m+2对任意x∈[0,2π]恒成立,求实数m的取值范围.
)≥m+2对任意x∈[0,2π]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且a5a6+a4a7=18,则log3a1+log3a2+…+log3a10=( )
A.5
B.9
C.log345
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5. 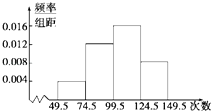
(1)求第四小组的频率;
(2)参加这次测试的学生人数是多少?
(3)在这次测试中,学生跳绳次数的中位数落在第几小组内?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com