
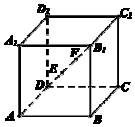
 如图,在正方体ABCD-A1B1C1D1中,AB=3$\sqrt{3}$,点E,F在线段DB1上,且DE=EF=FB1,点M是正方体表面上的一动点,点P,Q是空间两动点,若$\frac{|PE|}{|PF|}$=$\frac{|QE|}{|QF|}$=2且|PQ|=4,则$\overrightarrow{MP}$•$\overrightarrow{MQ}$的最小值为-$\frac{8}{3}$.
如图,在正方体ABCD-A1B1C1D1中,AB=3$\sqrt{3}$,点E,F在线段DB1上,且DE=EF=FB1,点M是正方体表面上的一动点,点P,Q是空间两动点,若$\frac{|PE|}{|PF|}$=$\frac{|QE|}{|QF|}$=2且|PQ|=4,则$\overrightarrow{MP}$•$\overrightarrow{MQ}$的最小值为-$\frac{8}{3}$. 分析 首先由由题意可得DB1=9,EF=3,在线段EF上取一点K,使得EK=2,FK=1,设KB1的中点为N,如图,由已知可得点P,Q在以KB1为直径的球N的表面上,球心为N,球的直径为4,由于|PQ|=4,故PQ是球N的直径,由向量的知识可知$\overrightarrow{MP}$•$\overrightarrow{MQ}$=${\overrightarrow{MN}}^{2}$-4,故要求$\overrightarrow{MP}$•$\overrightarrow{MQ}$的最小值,只需要求出|$\overrightarrow{MN}$|的最小值,结合图形解答即可
解答 解:如图,由题意可得DB1=9,EF=3,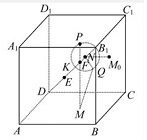
在线段EF上取一点K,使得EK=2,FK=1,
设KB1的中点为N,
由于$\frac{|PE|}{|PF|}$=$\frac{|QE|}{|QF|}$=2,则点P,Q在以KB1为直径的球N的表面上,球心为N,球的直径为4,
由于|PQ|=4,故PQ是球N的直径,
即$\overrightarrow{MP}$•$\overrightarrow{MQ}$=$\frac{1}{4}$($\overrightarrow{MP}$+$\overrightarrow{MQ}$)2-($\overrightarrow{MP}$-$\overrightarrow{MQ}$)2]=${\overrightarrow{MN}}^{2}$-$\frac{1}{4}$${\overrightarrow{QP}}^{2}$=${\overrightarrow{MN}}^{2}$-4,
故要求$\overrightarrow{MP}$•$\overrightarrow{MQ}$的最小值,只需要求出|$\overrightarrow{MN}$|的最小值,
设点N在平面BCC1B1内的射影为M0,则当M在M0处时,|$\overrightarrow{MN}$|有最小值$\frac{2}{9}$|$\overrightarrow{AB}$|=$\frac{2\sqrt{3}}{3}$,
此时${\overrightarrow{MN}}^{2}$-4=$\frac{4}{3}$-4=-$\frac{8}{3}$,
故答案为:-$\frac{8}{3}$
点评 本题考查了空间几何体,以及向量的有关知识,关键是判断出要求$\overrightarrow{MP}$•$\overrightarrow{MQ}$的最小值,只需要求出|$\overrightarrow{MN}$|的最小值,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\sqrt{2}$x | B. | y=±2x | C. | y=±$\frac{\sqrt{2}}{2}$x | D. | y=±$\frac{1}{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\sqrt{2})$ | B. | $(\sqrt{2},0)$ | C. | $(-\sqrt{2},\sqrt{2})$ | D. | $(\sqrt{2},\sqrt{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com