
【题目】在![]() 中,
中,![]() 且
且![]() ,
,![]() 边上的中线长为
边上的中线长为![]() ,则
,则![]() 的面积是________.
的面积是________.
【答案】![]()
【解析】
根据题意,将![]() 变形可得
变形可得![]() ,又由
,又由![]() ,则
,则![]() 可以变形为
可以变形为![]() ,分析可得
,分析可得![]() 的值,进而可得
的值,进而可得![]() 的值,分析可得,
的值,分析可得,![]() 为等腰三角形,设
为等腰三角形,设![]() 为
为![]() 中点,AD=
中点,AD=![]() ,设
,设![]() ,在△ACD中,由余弦定理可得cosC=
,在△ACD中,由余弦定理可得cosC=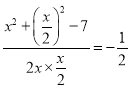 ,计算可得
,计算可得![]() 的值,由三角形面积公式计算可得答案.
的值,由三角形面积公式计算可得答案.
根据题意,![]() 中,
中,![]() ,则有
,则有![]() sinB=
sinB=![]() ,变形可得sinB=1+cosC,
,变形可得sinB=1+cosC,
则有cosC=sinB﹣1<0,则C为钝角,B为锐角.
又由A=![]() ,得B+C=
,得B+C=![]() ,则sinB=1+cosCsin(
,则sinB=1+cosCsin(![]() ﹣C)=1+cosCcos(C+
﹣C)=1+cosCcos(C+![]() )=﹣1,
)=﹣1,
又C为钝角,所以C=![]() ,B=
,B=![]() ﹣C=
﹣C=![]() ,
,
则在![]() 中,A=B=
中,A=B=![]() ,则有AC=BC,即
,则有AC=BC,即![]() 为等腰三角形,
为等腰三角形,
设D为BC中点,则AD=![]() ,设AC=x,则有cosC=
,设AC=x,则有cosC=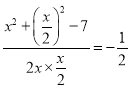 ,解得x=2,即AC=BC=2.
,解得x=2,即AC=BC=2.
则S△ABC=![]() ×AC×BC×sinC=
×AC×BC×sinC=![]() ×2×2×sin
×2×2×sin![]() =
=![]() .
.
故答案为![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,
,![]() 为椭圆
为椭圆![]() 上两点,圆
上两点,圆![]() .
.
(1)若![]() 轴,且满足直线
轴,且满足直线![]() 与圆
与圆![]() 相切,求圆
相切,求圆![]() 的方程;
的方程;
(2)若圆![]() 的半径为
的半径为![]() ,点
,点![]() 满足
满足![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得弦长的最大值.
截得弦长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三共有1000位学生,为了分析某次的数学考试成绩,采取随机抽样的方法抽取了200位高三学生的成绩进行统计分析得到如图所示频率分布直方图:
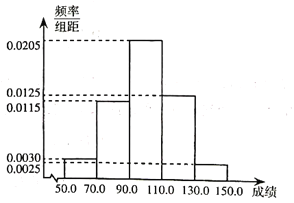
(1)计算这些学生成绩的平均值![]() 及样本方差
及样本方差![]() (同组的数据用该组区间的中点值代替);
(同组的数据用该组区间的中点值代替);
(2)由频率分布直方图认为,这次成绩X近似服从正态分布![]() ,其中μ近似为样本平均数
,其中μ近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)求![]() ;
;
(ii)从高三学生中抽取10位学生进行面批,记![]() 表示这10位学生成绩在
表示这10位学生成绩在![]() 的人数,利用(i)的结果,求数学期望
的人数,利用(i)的结果,求数学期望![]() .
.
附:![]() ;
;
若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学举办“父母养育我,我报父母恩”的活动,对六个年级(一年级到六年级的年级代码分别为1,2…,6)的学生给父母洗脚的百分比y%进行了调查统计,绘制得到下面的散点图.
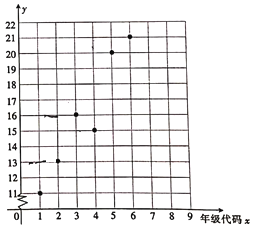
(1)由散点图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)建立y关于x的回归方程,并据此预计该校学生升入中学的第一年(年级代码为7)给父母洗脚的百分比.
附注:参考数据:![]()
参考公式:相关系数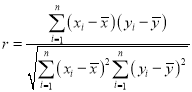 ,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程
,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程![]() 中斜率与截距的最小二乘估计公式分别为
中斜率与截距的最小二乘估计公式分别为![]() =
=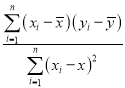 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂预购软件服务,有如下两种方案:
方案一:软件服务公司每日收取工厂60元,对于提供的软件服务每次10元;
方案二:软件服务公司每日收取工厂200元,若每日软件服务不超过15次,不另外收费,若超过15次,超过部分的软件服务每次收费标准为20元.
(1)设日收费为![]() 元,每天软件服务的次数为
元,每天软件服务的次数为![]() ,试写出两种方案中
,试写出两种方案中![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)该工厂对过去100天的软件服务的次数进行了统计,得到如图所示的条形图,依据该统计数据,把频率视为概率,从节约成本的角度考虑,从两个方案中选择一个,哪个方案更合适?请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂销售部以箱为单位销售某种零件,每箱的定价为200元,低于100箱按原价销售;不低于100箱通过双方议价,买方能以优惠![]() 成交的概率为0.6,以优惠
成交的概率为0.6,以优惠![]() 成交的概率为0.4.
成交的概率为0.4.
(1)甲、乙两单位都要在该厂购买150箱这种零件,两单位各自达成的成交价相互独立,求甲单位优惠比例不低于乙单位优惠比例的概率;
(2)某单位需要这种零件650箱,求购买总价![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD所在平面垂直于直角梯形ABPE所在平面,EP![]() ,BP=2,AD=AE=1,AE⊥EP,AE∥BP,G,F分别是BP,BC的中点.
,BP=2,AD=AE=1,AE⊥EP,AE∥BP,G,F分别是BP,BC的中点.
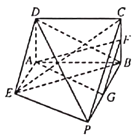
(1)求证:平面AFG∥平面PCE;
(2)求四棱锥D﹣ABPE的体积与三棱锥P﹣BCD的体积之比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com