
【题目】已知圆![]() ,圆心为
,圆心为![]() ,定点
,定点![]() ,
, ![]() 为圆
为圆![]() 上一点,线段
上一点,线段![]() 上一点
上一点![]() 满足
满足![]() ,直线
,直线![]() 上一点
上一点![]() ,满足
,满足![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)![]() 为坐标原点,
为坐标原点, ![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与
与![]() 相切,并与轨迹
相切,并与轨迹![]() 交于不同的两点
交于不同的两点![]() .当
.当![]() 且满足
且满足![]() 时,求
时,求![]() 面积
面积![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)  .
.
【解析】试题分析:(Ⅰ)分析题意可得点![]() 满足的几何条件,根据椭圆的定义可得轨迹,从而可求得轨迹方程;(Ⅱ)先由直线
满足的几何条件,根据椭圆的定义可得轨迹,从而可求得轨迹方程;(Ⅱ)先由直线![]() 与
与![]() 相切得到
相切得到![]() ,将直线方程与椭圆方程联立,并结合一元二次方程根与系数的关系可得
,将直线方程与椭圆方程联立,并结合一元二次方程根与系数的关系可得![]() ,由
,由![]() 且
且![]() ,进一步得到k的范围,最后根据三角形面积公式并结合函数的单调性求
,进一步得到k的范围,最后根据三角形面积公式并结合函数的单调性求![]() 的取值范围。
的取值范围。
试题解析:
(Ⅰ)∵![]()
∴![]() 为线段
为线段![]() 中点
中点
∵![]()
∴![]() 为线段
为线段![]() 的中垂线
的中垂线
∴![]()
∵![]()
∴由椭圆的定义可知![]() 的轨迹是以
的轨迹是以![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆,
的椭圆,
设椭圆的标准方程为![]() ,
,
则![]() ,
, ![]() ,
,
∴![]() 。
。
∴点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() 。
。
(Ⅱ)∵圆![]() 与直线
与直线![]() 相切,
相切,
∴![]() ,即
,即![]() ,
,
由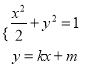 ,消去
,消去![]() .
.
∵直线![]() 与椭圆交于两个不同点,
与椭圆交于两个不同点,
∴![]() ,
,
将![]() 代入上式,可得
代入上式,可得![]() ,
,
设![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
,
∴![]()
![]() ,
,
∴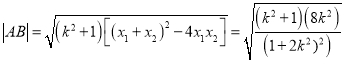
∴![]() ,
,
∵![]() ,解得
,解得![]() .满足
.满足![]() 。
。
又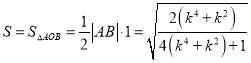 ,
,
设![]() ,则
,则![]() .
.
∴![]()
 ,
,
∴![]()
故![]() 面积
面积![]() 的取值范围为
的取值范围为 。
。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知(2x-3y)9=a0x9+a1x8y+a2x7y2+…+a9y9,求:
(1)各项系数之和;
(2)所有奇数项系数之和;
(3)系数绝对值的和;
(4)分别求出奇数项的二项式系数之和与偶数项的二项式系数之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)△ABC中,角A,B,C所对的边分别为a,b,c.已知a=3,cos A=![]() ,B=A+
,B=A+![]() .
.
(1)求b的值;
(2)求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
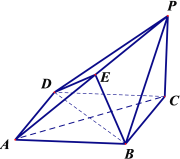
【题目】如图,在四棱锥![]() 中, 底面
中, 底面![]() 为菱形,
为菱形,![]() 平面
平面![]() ,点
,点![]() 在棱
在棱![]() 上.
上.
(Ⅰ)求证:直线![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 平面
平面![]() ,求证:
,求证:![]() ;
;
(Ⅲ)是否存在点![]() ,使得四面体
,使得四面体![]() 的体积等于四面体
的体积等于四面体![]() 的体积的
的体积的![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两定点![]() ,
, ![]() 和一动点
和一动点![]() ,给出下列结论:
,给出下列结论:
①若![]() ,则点
,则点![]() 的轨迹是椭圆;
的轨迹是椭圆;
②若![]() ,则点
,则点![]() 的轨迹是双曲线;
的轨迹是双曲线;
③若![]() ,则点
,则点![]() 的轨迹是圆;
的轨迹是圆;
④若![]() ,则点
,则点![]() 的轨迹关于原点对称;
的轨迹关于原点对称;
⑤若直线![]() 与
与![]() 斜率之积等于
斜率之积等于![]() ,则点
,则点![]() 的轨迹是椭圆(除长轴两端点).
的轨迹是椭圆(除长轴两端点).
其中正确的是__________(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,甲船以每小时30![]() 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10![]() 海里.问:乙船每小时航行多少海里?
海里.问:乙船每小时航行多少海里?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题的真假,并说明理由.
(1)x∈R,都有x2-x+1>![]() ;
;
(2)α,β,使cos(α-β)=cos α-cos β;
(3)x,y∈N,都有(x-y)∈N;
(4)x,y∈Z,使![]() x+y=3.
x+y=3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,(1)已知a=![]() ,b=
,b=![]() ,B=45°,求A、C、c;
,B=45°,求A、C、c;
(2)已知sin A∶sin B∶sin C=(![]() +1)∶(
+1)∶(![]() -1)∶
-1)∶![]() ,求最大角.
,求最大角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com