考点:异面直线及其所成的角,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(1)利用正方体的结构特征和平行线的定义能求出在正方体AC′中,与AC平行的面对角线.
(2)利用正方体的结构特征和异面线的定义能求出在正方体AC′中,与AC异面的面对角线.
(3)由B′D′∥BD,BD⊥AC,得到直线AC与B′D′所成的角为90°.
(4)由CC′∥BB′,得∠A′BB′是直线BA′和CC′所成的角,由此能求出直线BA′和CC′所成的角.
(5)由B′C∥A′D,得∠BA′D是直线BA′与B′C所成的角,由此能求出直线BA′与B′C所成的角.
解答:
解:(1)在正方体AC′中,与AC平行的面对角线是A′C′.
(2)正方体AC′中,与AC异面的面对角线是BC,A′D,B′D′,DC,A′B.
(3)∵B′D′∥BD,BD⊥AC,
∴直线AC与B′D′所成的角为90°.
(4)∵CC′∥BB′,∴∠A′BB′是直线BA′和CC′所成的角,
∵∠A′BB′=45°,∴直线BA′和CC′所成的角为45°.
(5)∵B′C∥A′D,∴∠BA′D是直线BA′与B′C所成的角,
∵∠BA′D=60°,∴直线BA′与B′C所成的角为60°.
点评:本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力,在立体几何中找平行线是解决问题的一个重要技巧,这个技巧就是通过三角形的中位线找平行线,如果试题的已知中涉及到多个中点,则找中点是出现平行线的关键技巧.

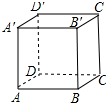 如图,正方体AC′的棱长为a.
如图,正方体AC′的棱长为a.

 阅读快车系列答案
阅读快车系列答案