[题目]已知函数在区间上有最大值和最小值.设(1)求的值(2)若不等式在上有解,求实数的取值范围;(3)若有三个不同的实数解,求实数的取值范围. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知函数在区间上有最大值和最小值.设

（1）求的值

（2）若不等式在上有解,求实数的取值范围;

（3）若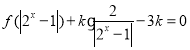有三个不同的实数解,求实数的取值范围.

【答案】（1）.（2）（3）

【解析】

(1)由函数,所以在区间上是增函数,故,由此解得的值;

(2)由(1)可得,所以在上有解,等价于在上有解, 即在上有解, 令,则,即可求得的取值范围;

(3)原方程可化为,令则,有两个不同的实数解,其中,或,即可求得实数的取值范围.

(1)函数,

在区间上是增函数,

故:,解得.

(2)由(1)可得,

在上有解

等价于在上有解

即在上有解

令,则

,故

记,

的取值范围为

(3)原方程可化为

令则

有两个不同的实数解

其中,或

记

则——①,解得

或——②,不等式组②无实数解.

实数的取值范围为.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】设函数

（1）如果，那么实数___；

（2）如果函数有且仅有两个零点，那么实数的取值范围是___.

【答案】或4；

【解析】

试题分析：由题意，解得或；

第二问如图：

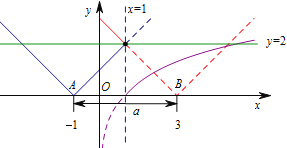
的图象是由两条以为顶点的射线组成，当在A,B 之间（包括不包括）时，函数和有两个交点，即有两个零点．所以的取值范围为．

考点：1.分段函数值；2.函数的零点.

【题型】填空题
【结束】
15

【题目】已知函数的部分图象如图所示．

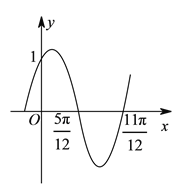
（）求函数的解析式．

（）求函数在区间上的最大值和最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知直线，则下列结论正确的是（）

A.直线的倾斜角是B.若直线则

C.点到直线的距离是D.过与直线平行的直线方程是

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某中学有初中学生1800人，高中学生1200人.为了解学生本学期课外阅读时间，现采用分层抽样的方法，从中抽取了100名学生，先统计了他们课外阅读时间，然后按“初中学生”和“高中学生”分为两组，再将每组学生的阅读时间（单位：小时）分为5组：[0，10），[10，20），[20，30），[30，40），[40，50]，并分别加以统计，得到如下图所示的频率分布直方图.

（I）写出a的值；

（II）试估计该校所有学生中，阅读时间不小于30个小时的学生人数；

（III）从阅读时间不足10个小时的样本学生中随机抽取3人，并用X表示其中初中生的人数，求X的分布列和数学期望.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】汉字听写大会不断创收视新高，为了避免“书写危机”，弘扬传统文化，某市大约10万名市民进行了汉字听写测试现从某社区居民中随机抽取50名市民的听写测试情况，发现被测试市民正确书写汉字的个数全部在160到184之间，将测试结果按如下方式分成六组：第1组，第2组，，第6组，如图是按上述分组方法得到的频率分布直方图．