
 某山体外围有两条相互垂直的直线型公路,为开发山体资源,修建一条连接两条公路沿山区边界的直线型公路.记两条相互垂直的公路为l1,l2,山区边界曲线为C,计划修建的公路为L.如图所示,M,N为C的两个端点,测得点M到l1,l2的距离分别为5千米和80千米,点N到l1的距离为100千米,以l1,l2 所在的直线分别为x、y轴建立平面直角坐标系xOy,假设曲线C符合函数y=$\frac{a}{x}$模型(其中a为常数).
某山体外围有两条相互垂直的直线型公路,为开发山体资源,修建一条连接两条公路沿山区边界的直线型公路.记两条相互垂直的公路为l1,l2,山区边界曲线为C,计划修建的公路为L.如图所示,M,N为C的两个端点,测得点M到l1,l2的距离分别为5千米和80千米,点N到l1的距离为100千米,以l1,l2 所在的直线分别为x、y轴建立平面直角坐标系xOy,假设曲线C符合函数y=$\frac{a}{x}$模型(其中a为常数).分析 (1)①由题知M(5,80)代入y=$\frac{a}{x}$,则a=400,进而求出y=$\frac{400}{x}$,得出坐标N(100,4),利用导数求出斜率,得出直线的方程$y=-\frac{400}{t^2}x+\frac{800}{t}$,进而求出与坐标轴的交点A(0,$\frac{800}{t}$),B(2t,0),利用勾股定理可得$f(t)=\sqrt{{{(\frac{800}{t})}^2}+{{(2t)}^2}}$(t∈[5,100]);
②运用基本不等式可得最小值,注意求出等号成立的条件;
(2)山体与x=5,x=100之间的面积为$\int_5^{100}{\frac{400}{x}dx}=400ln20$,得出山体与L1、L2围成的面积是400+400ln20,进而得出绿化带的面积是400+400ln20-800=400ln20-400.
解答 解:(1)①由题意M(5,80)代入y=$\frac{a}{x}$,则a=400,
∴y=$\frac{400}{x}$,N(100,4),
∴定义域为[5,100].
∴P(t,$\frac{400}{t}$),
∵$y'=-\frac{400}{x^2}$,则公路l的方程:$y=-\frac{400}{t^2}x+\frac{800}{t}$,
令x=0,可得y=$\frac{800}{t}$;令y=0,可得x=2t.
∴$f(t)=\sqrt{{{(\frac{800}{t})}^2}+{{(2t)}^2}}$(t∈[5,100]);
②A(0,$\frac{800}{t}$),B(2t,0),
$f(t)=\sqrt{{{(\frac{800}{t})}^2}+{{(2t)}^2}}$=$\sqrt{\frac{640000}{t^2}+4{t^2}}≥3200$,
当且仅当t=20∈[5,100]时等号成立,
所以当t为20时,公路l的长度最短长度是3200千米;
(2)山体与x=5,x=100之间的面积为
${∫}_{5}^{100}$$\frac{400}{x}$dx=400lnx|${\;}_{5}^{100}$=400(ln100-ln5)=400ln20,
山体与L1、L2围成的面积是400+400ln20,
L与y,x轴交点分别是A(0,40),B(40,0),公路与L1、L2围成的面积是800,
所以绿化带的面积是400+400ln20-800=400ln20-400(平方公里).
答:当t为20时,公路L的长度最短,最短长度是3200千米;
在公路长度最短时,需在公路L与山体之间修建绿化带的面积是400ln20-400平方公里.
点评 本题考查了利用导数求直线方程和积分的应用,考查运算求解能力,难点是对题意的理解.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 63 | B. | 31 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
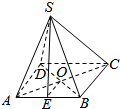 如图,S-ABCD是正四棱锥,已知底面边长AB=6cm,侧棱SA=3$\sqrt{5}$cm,求该正四棱锥的侧面SAB的斜高SE和底面AC所成角的大小.
如图,S-ABCD是正四棱锥,已知底面边长AB=6cm,侧棱SA=3$\sqrt{5}$cm,求该正四棱锥的侧面SAB的斜高SE和底面AC所成角的大小.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 质量指标值分组 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 2 | 3 | 4 | 5 | 4 | 2 |
| 质量指标值分组 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 0.15 | 0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点,沿直线BD将△BCD翻折成△BC′D,使得平面BC′D⊥平面ABD.
已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点,沿直线BD将△BCD翻折成△BC′D,使得平面BC′D⊥平面ABD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com