
 年龄段的市民回答第一个问题的正确率为
年龄段的市民回答第一个问题的正确率为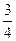 ,
, 年龄段的市民回答第二个问题正确率为
年龄段的市民回答第二个问题正确率为 .
. ,42岁大人回答问题二的正确率为
,42岁大人回答问题二的正确率为 ,则13岁孩子回答问题一的不正确率为
,则13岁孩子回答问题一的不正确率为 ,42岁大人回答问题二的不正确率为
,42岁大人回答问题二的不正确率为 ......................................... (1分)
......................................... (1分) 元,则
元,则 的可取值为0,20,30,50...................... (3分)
的可取值为0,20,30,50...................... (3分) ;.......................................................... (5分)
;.......................................................... (5分) ;......................................................... (7分)
;......................................................... (7分) ;.......................................................... (9分)
;.......................................................... (9分) .......................................................... (11分)
.......................................................... (11分) | 0 | 20 | 30 | 50 |
 |  | 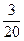 |  |  |
 ................................ (13分)
................................ (13分) ..................................... (14分)
..................................... (14分)

科目:高中数学 来源:不详 题型:解答题
 的概率分布列
的概率分布列查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .
. .
. 的回归直线方程是:
的回归直线方程是: ,使代数式
,使代数式



 的值最小时,
的值最小时, ,
, ,(
,( 、
、 分别是这三组数据的横、纵坐标的平均数)
分别是这三组数据的横、纵坐标的平均数)| x | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 6 | 5 | 6.2 | 8 | 7.1 | 8.6 |
 ,即称
,即称 为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,对周一和周二的单词每个能默写对的概率为
,对周一和周二的单词每个能默写对的概率为 ;现已知老师从周一到周四每天的单词中各抽取了一个单词进行检测,求该学生能默写对的单词数
;现已知老师从周一到周四每天的单词中各抽取了一个单词进行检测,求该学生能默写对的单词数 的分布列和期望.
的分布列和期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 拐入同一公路时,需要有一车等待.已知甲车拐入需要的时间为2分钟,乙车拐入需要的时间为1分钟,倘若甲、乙两车都在某5分
拐入同一公路时,需要有一车等待.已知甲车拐入需要的时间为2分钟,乙车拐入需要的时间为1分钟,倘若甲、乙两车都在某5分 钟内到达转弯路口,则至少有一辆车转弯时需要
钟内到达转弯路口,则至少有一辆车转弯时需要 等待的概率
等待的概率 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com