
【题目】已知函数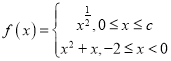 ,
,
其中c>0.那么f(x)的零点是________;若f(x)的值域是![]() ,则c的取值范围是________.
,则c的取值范围是________.
【答案】-1和0 (0,4]
【解析】
根据分段函数的概念,分x为正数和负数两种情况讨论,分别解方程即可得到么f(x)的零点.
根据二次函数的图象与性质,求出当x∈[-2,0)时,函数f(x)的值域恰好是[![]() ,2],所以当0≤x≤c时,f(x)=
,2],所以当0≤x≤c时,f(x)=![]() 的最大值小于等于2,即可解出实数c的取值范围.
的最大值小于等于2,即可解出实数c的取值范围.
当x≥0时,令![]() =0,得x=0;
=0,得x=0;
当x<0时,令x2+x=0,得x=-1或x=0(舍去)
∴f(x)的零点是-1和0
∵函数y=x2+x=![]() ,在区间[-2,-
,在区间[-2,-![]() )上是减函数,在区间(-
)上是减函数,在区间(-![]() ,0)上是增函数
,0)上是增函数
∴当x∈[-2,0)时,函数f(x)最小值为f(-![]() )=-
)=-![]() ,最大值是f(-2)=2
,最大值是f(-2)=2
∵当0≤x≤c时,f(x)=![]() 是增函数且值域为[0,
是增函数且值域为[0,![]() ]
]
∵f(x)的值域是[![]() ,2],∴
,2],∴ ![]() ≤2,即0<c≤4
≤2,即0<c≤4


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3-3x2+1,g(x)=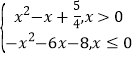 ,若方程g[f(x)]-a=0(a>0)有6个实数根(互不相同),则实数a的取值范围是______.
,若方程g[f(x)]-a=0(a>0)有6个实数根(互不相同),则实数a的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是( )
A.若“![]() ”为假命题,则“
”为假命题,则“![]() ”为假命题
”为假命题
B.“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
C.命题“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
D.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们把定义在![]() 上,且满足
上,且满足![]() (其中常数
(其中常数![]() ,
,![]() 满足
满足![]() ,
,![]() ,
,![]() )的函数叫做似周期函数.
)的函数叫做似周期函数.
(1)若某个似周期函数![]() 满足
满足![]() 且图像关于直线
且图像关于直线![]() 对称,求证:函数
对称,求证:函数![]() 是偶函数;
是偶函数;
(2)当![]() ,
,![]() 时,某个似周期函数在
时,某个似周期函数在![]() 时的解析式为
时的解析式为![]() ,求函数
,求函数![]() ,
,![]() 的解析式;
的解析式;
(3)对于确定的![]() 且当
且当![]() 时,
时,![]() ,试研究似周期函数
,试研究似周期函数![]() 在区间
在区间![]() 上是否可能是单调函数?若可能,求出
上是否可能是单调函数?若可能,求出![]() 的取值范围;若不可能,请说明理由.
的取值范围;若不可能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于集合![]() ,定义函数
,定义函数![]() 对于两个集合
对于两个集合![]() ,定义集合
,定义集合![]() . 已知
. 已知![]() ,
, ![]() .
.
(Ⅰ)写出![]() 和
和![]() 的值,并用列举法写出集合
的值,并用列举法写出集合![]() ;
;
(Ⅱ)用![]() 表示有限集合
表示有限集合![]() 所含元素的个数,求
所含元素的个数,求![]() 的最小值;
的最小值;
(Ⅲ)有多少个集合对![]() ,满足
,满足![]() ,且
,且![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且2ccosB=2a+b.
(1)求角C的大小;
(2)若△ABC的面积等于![]() ,求ab的最小值.
,求ab的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图的折线图是某超市2018年一月份至五月份的营业额与成本数据,根据该折线图,下列说法正确的是( )
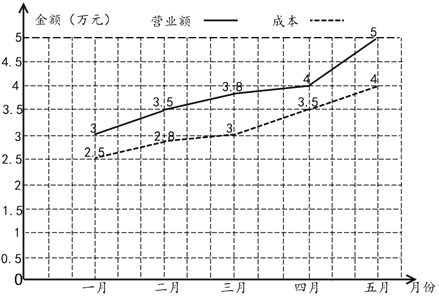
A.该超市2018年的前五个月中三月份的利润最高
B.该超市2018年的前五个月的利润一直呈增长趋势
C.该超市2018年的前五个月的利润的中位数为0.8万元
D.该超市2018年前五个月的总利润为3.5万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com