

【题目】某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大.已知对这两种产品有直接限制的因素是资金和劳动力,经调查,得到关于这两种产品的有关数据如下表:
资金 | 每台产品所需资金(百元) | 月资金供应量 (百元) | |
空调机 | 洗衣机 | ||
成本 | 30 | 20 | 300 |
劳动力(工资) | 5 | 10 | 110 |
每台产品利润 | 6 | 8 | |
试问:怎样确定两种货物的月供应量,才能使总利润最大?最大利润是多少?
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 为实数.
为实数.
(1)是否存在![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(2)若集合![]() 中恰有5个元素,求实数
中恰有5个元素,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是定义在
是定义在![]() 上的函数,如果存在
上的函数,如果存在![]() 点,对函数
点,对函数![]() 的图象上任意点
的图象上任意点![]() ,
,![]() 关于点
关于点![]() 的对称点
的对称点![]() 也在函数
也在函数![]() 的图象上,则称函数
的图象上,则称函数![]() 关于点
关于点![]() 对称,
对称,![]() 称为函数
称为函数![]() 的一个对称点,对于定义在
的一个对称点,对于定义在![]() 上的函数
上的函数![]() ,可以证明点
,可以证明点![]() 是
是![]() 图象的一个对称点的充要条件是
图象的一个对称点的充要条件是![]() ,
,![]() .
.
(1)求函数![]() 图象的一个对称点;
图象的一个对称点;
(2)函数![]() 的图象是否有对称点?若存在则求之,否则说明理由;
的图象是否有对称点?若存在则求之,否则说明理由;
(3)函数![]() 的图象是否有对称点?若存在则求之,否则说明理由.
的图象是否有对称点?若存在则求之,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有30名男职员和20名女职员,公司进行了一次全员参与的职业能力测试,现随机询问了该公司5名男职员和5名女职员在测试中的成绩(满分为30分),可知这5名男职员的测试成绩分别为16,24,18,
22,20,5名女职员的测试成绩分别为18,23,23,18,23,则下列说法一定正确的是( )
A. 这种抽样方法是分层抽样
B. 这种抽样方法是系统抽样
C. 这5名男职员的测试成绩的方差大于这5名女职员的测试成绩的方差
D. 该测试中公司男职员的测试成绩的平均数小于女职员的测试成绩的平均数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(1)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(2)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、乙两女生被抽到的人数为X,求X的分布列及数学期望E(X).
附表及公式:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,货轮在海上以35n mile/h的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为![]() 的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为
的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为![]() .半小时后,货轮到达C点处,观测到灯塔A的方位角为
.半小时后,货轮到达C点处,观测到灯塔A的方位角为![]() .求此时货轮与灯塔之间的距离.
.求此时货轮与灯塔之间的距离.
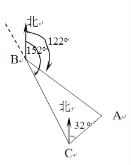
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若对![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)记![]() ,那么当
,那么当![]() 时,是否存在区间
时,是否存在区间![]() 使得函数在区间
使得函数在区间![]() 上的值域恰好为
上的值域恰好为![]() ?若存在,请求出区间
?若存在,请求出区间![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一座大桥既是交通拥挤地段,又是事故多发地段,为了保证安全,交通部门规定:大桥上的车距![]() 与车速
与车速![]() 和车长
和车长![]() 的关系满足
的关系满足![]() 为正的常数).假定车身长为
为正的常数).假定车身长为![]() ,当车速为
,当车速为![]() 时,车距为
时,车距为![]() 个车身长.
个车身长.
(1)写出车距![]() 关于车速
关于车速![]() 的函数关系式;
的函数关系式;
(2)应规定怎样的车速,才能使大桥上每小时通过的车辆最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com