
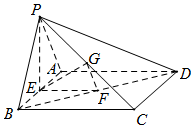
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F,G分别是AB,BD,PC的中点,PE⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F,G分别是AB,BD,PC的中点,PE⊥底面ABCD.分析 (Ⅰ)连结AC.证明GF∥PA.推出GF∥平面PAD.然后证明EF∥AD.得到EF∥平面PAD.即可证明平面EFG∥平面PAD.
(Ⅱ)存在λ,$λ=\frac{{\sqrt{2}}}{2}$,即$PB=\frac{{\sqrt{2}}}{2}AB$时,平面PBC⊥平面PAD.
方法一:证明PE⊥BC,PE⊥AB.得到BC⊥平面PAB.说明PA=PB.当PA⊥PB,$PA=PB=\frac{{\sqrt{2}}}{2}AB$时,PA⊥平面PBC.然后求解即可.
方法二:过点P作PQ∥BC.说明PQ,AD共面,推出PE⊥BC.说明∠APB是平面PAD和平面PBC所成二面角的平面角.然后通过$PA=\frac{{\sqrt{2}}}{2}AB$.即$PB=\frac{{\sqrt{2}}}{2}AB$时,说明平面PBC⊥平面PAD..
解答 (本题满分9分)
(Ⅰ)证明:连结AC.
∵底面ABCD是矩形,F是BD中点,
∴F也是AC的中点.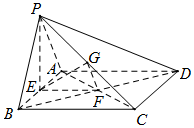
∵G是PC的中点,∴GF是△PAC的中位线,
∴GF∥PA.
∵GF?平面PAD,PA?平面PAD,
∴GF∥平面PAD.
∵E是AB中点,F是BD中点,
∴EF是△ABD的中位线,
∴EF∥AD.
∵EF?平面PAD,AD?平面PAD,
∴EF∥平面PAD.
∵GF∥平面PAD,EF∥平面PAD,EF∩FG=F,
∴平面EFG∥平面PAD. …(5分)
(Ⅱ)解:存在λ,$λ=\frac{{\sqrt{2}}}{2}$,即$PB=\frac{{\sqrt{2}}}{2}AB$时,平面PBC⊥平面PAD.
方法一:∵PE⊥底面ABCD,BC?底面ABCD,AB?底面ABCD, ∴PE⊥BC,PE⊥AB.
∴PE⊥BC,PE⊥AB.
∵底面ABCD是矩形,
∴AB⊥BC.
∵PE∩AB=E,
∴BC⊥平面PAB.
∵PA?平面PAB,
∴PA⊥BC.
∵PE⊥AB,E为AB的中点,
∴PA=PB.
当PA⊥PB,即$PA=PB=\frac{{\sqrt{2}}}{2}AB$时,
∴PA⊥平面PBC.
∵PA?平面PAD,
∴平面PAD⊥平面PBC.此时 $λ=\frac{{\sqrt{2}}}{2}$.…(9分)
方法二:过点P作PQ∥BC.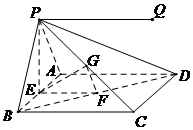
∴PQ,BC共面,即PQ?平面PBC.
∵底面ABCD是矩形,
∴AD∥BC.
∵PQ∥BC,
∴PQ∥AD.
∴PQ,AD共面,即PQ?平面PAD.
∴平面PBC∩平面PAD=PQ.
∵PE⊥底面ABCD,BC?底面ABCD,
∴PE⊥BC.
∵底面ABCD是矩形,
∴AB⊥BC.
∵PQ∥BC,
∴PE⊥PQ,AB⊥PQ.
∵PE∩AB=E,
∴PQ⊥平面PAB.
∵PA?平面PAB,PB?平面PAB,
∴PA⊥PQ,PB⊥PQ,
∴∠APB是平面PAD和平面PBC所成二面角的平面角.
∵平面PAD⊥平面PBC,
∴∠APB=90°.
∵PE⊥AB,E为AB的中点,
∴PA=PB.
∴△PAB是等腰直角三角形.
∴$PA=\frac{{\sqrt{2}}}{2}AB$.即$PB=\frac{{\sqrt{2}}}{2}AB$时,平面PBC⊥平面PAD. …(9分)
点评 本题考查平面与平面平行于垂直的判定定理以及性质定理的应用,存在性问题的处理方法,考查空间想象能力以及计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)=14 | B. | f(1)>14 | C. | f(1)≤14 | D. | f(1)≥14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{7}{4}$ | C. | $\frac{11}{4}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com