
【题目】在我国古代数学名著《九章算术》中将由四个直角三角形组成的四面体称为“鳖臑”.已知三棱维![]() 中,
中,![]() 底面
底面![]() .
.

(1)从三棱锥![]() 中选择合适的两条棱填空_________⊥________,则该三棱锥为“鳖臑”;
中选择合适的两条棱填空_________⊥________,则该三棱锥为“鳖臑”;
(2)如图,已知![]() 垂足为
垂足为![]() ,垂足为
,垂足为![]() .
.
(i)证明:平面![]() ⊥平面
⊥平面![]() ;
;
(ii)作出平面![]() 与平面
与平面![]() 的交线
的交线![]() ,并证明
,并证明![]() 是二面角
是二面角![]() 的平面角.(在图中体现作图过程不必写出画法)
的平面角.(在图中体现作图过程不必写出画法)
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】东莞市公交公司为了方便广大市民出行,科学规划公交车辆的投放,计划在某个人员密集流动地段增设一个起点站,为了研究车辆发车的间隔时间![]() 与乘客等候人数
与乘客等候人数![]() 之间的关系,选取一天中的六个不同的时段进行抽样调查,经过统计得到如下数据:
之间的关系,选取一天中的六个不同的时段进行抽样调查,经过统计得到如下数据:
间隔时间( | 8 | 10 | 12 | 14 | 16 | 18 |
等候人数( | 16 | 19 | 23 | 26 | 29 | 33 |
调查小组先从这6组数据中选取其中的4组数据求得线性回归方程,再用剩下的2组数据进行检验,检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若两组差值的绝对值均不超过1,则称所求的回归方程是“理想回归方程”.
的差,若两组差值的绝对值均不超过1,则称所求的回归方程是“理想回归方程”.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: ,
,
(1)若选取的是前4组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判断(1)中的方程是否是“理想回归方程”:
(3)为了使等候的乘客不超过38人,试用(1)中方程估计间隔时间最多可以设置为多少分钟?
查看答案和解析>>
科目:高中数学 来源: 题型:
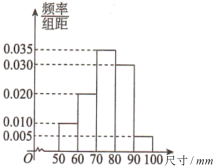
【题目】某工厂为检验车间一生产线工作是否正常,现从生产线中随机抽取一批零件样本,测量它们的尺寸(单位:![]() )并绘成频率分布直方图,如图所示.根据长期生产经验,可以认为这条生产线正常状态下生产的零件尺寸
)并绘成频率分布直方图,如图所示.根据长期生产经验,可以认为这条生产线正常状态下生产的零件尺寸![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为零件样本平均数
近似为零件样本平均数![]() ,
,![]() 近似为零件样本方差
近似为零件样本方差![]() .
.
(1)求这批零件样本的![]() 和
和![]() 的值(同一组中的数据用该组区间的中点值作代表);
的值(同一组中的数据用该组区间的中点值作代表);
(2)假设生产状态正常,求![]() ;
;
(3)若从生产线中任取一零件,测量其尺寸为![]() ,根据
,根据![]() 原则判断该生产线是否正常?
原则判断该生产线是否正常?
附:![]() ;若
;若![]() ,则
,则![]() ,
, ![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定圆![]() :
:![]() ,动圆
,动圆![]() 过点
过点![]()
![]() 且与圆
且与圆![]() 相切,记圆心
相切,记圆心![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知直线![]()
![]() 交圆
交圆![]() 于
于![]() 两点.
两点.![]() 是曲线
是曲线![]() 上两点,若四边形
上两点,若四边形![]() 的对角线
的对角线![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机支付也称为移动支付![]() ,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.
,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.
组数 | 第l组 | 第2组 | 第3组 | 第4组 | 第5组 |
分组 |
|
|
|
|
|
频数 | 20 | 36 | 30 | 10 | 4 |

(1)求![]() ;
;
(2)从第l,3,4组中用分层抽样的方法抽取6人,求第l,3,4组抽取的人数:
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,如表是该地一建设银行连续五年的储蓄存款(年底余额),如表1
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理,![]() 得到表2:
得到表2:
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(1)求z关于t的线性回归方程;
(2)通过(1)中的方程,求出y关于x的回归方程;
(3)用所求回归方程预测到2010年年底,该地储蓄存款额可达多少?
附:对于线性回归方程![]() ,
,
其中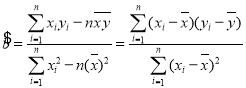 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个人下半身长(肚脐至足底)与全身长的比近似为![]() (
(![]() ,称为黄金分割比),堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好,若某人着装前测得头顶至肚脐长度为72
,称为黄金分割比),堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好,若某人着装前测得头顶至肚脐长度为72![]() ,肚脐至足底长度为103
,肚脐至足底长度为103![]() ,根据以上数据,作为形象设计师的你,对TA的着装建议是( )
,根据以上数据,作为形象设计师的你,对TA的着装建议是( )
A.身材完美,无需改善B.可以戴一顶合适高度的帽子
C.可以穿一双合适高度的增高鞋D.同时穿戴同样高度的增高鞋与帽子
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com