考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)利用导数判断函数的单调性,即可得出f(x)≥f(0)=0;
(Ⅱ)令g(x)=
,利用导数判断函数的单调性,求出函数的最大值、最小值,即可得出a≤1,b≥e-1,即可得出结论;
(Ⅲ)由题意可得只需证f(x)>x-
,即证(x-1)e
x-x+
>0在[0,1]上恒成立.令k(x)=(x-1)e
x-x+
,利用导数判断函数的单调性,得出最值,即可得出结论.
解答:
解:(Ⅰ)f′(x)=xe
x≥0 即f(x)在[0,1]上单调递增.…(2分)
所以f(x)≥f(0)=0,即结论成立.…(3分)
(Ⅱ)令g(x)=
,则g′(x)=
≥0,x∈(0,1)…(4分)
所以,当x∈(0,1)时,g(x)<g(1)=e-1,
要使
<b,只需b≥e-1 …(5分)
要使
>a成立,只需e
x-ax-1>0在x∈(0,1)恒成立.…(6分)
令h(x)=e
x-ax-1x∈(0,1)
则h′(x)=e
x-a,由x∈(0,1),e
x∈(1,e),
当a≤1时,h′(x)≥0 此时x∈(0,1),有h(x)>h(0)=0成立.
所以a≤1满足条件.
当a≥e时,h′(x)≤0,此时x∈(0,1)有h(x)<h(0)=0,
不符合题意,舍去.
当1<a<e时,令h′(x)=0,得x=lna,
可得当x∈(0,lna)时,h′(x)≤0.即x∈(0,lna)时,h(x)<h(0)=0,
不符合题意舍去.
综上,a≤1 …(9分)
又b≥e-1,所以b-a的最小值为e-2.…(10分)
(Ⅲ)由题意只需证f(x)>x-
,即证(x-1)e
x-x+
>0在[0,1]上恒成立.
令k(x)=(x-1)e
x-x+
,k′(x)=xe
x-1 …(11分)
k
″(x)=(x+1)e
x>0,即k′(x)在[0,1]上单调递增.
又
k′()<0,k′(1)>0,所以k′(x)在[0,1]有唯一的解,记为x
0,
x0∈(,1)且
x0ex0-1=0,即
ex0=…(12分)
可得当x∈(0,x
0)时,k′(x)≤0,当x∈(x
0,1)时,k′(x)≥0,
所以只需最小值k(x
0)=(x
0-1)
ex0-x
0+
=
-(
x0+) …(13分)
易得
x0+<
,x
0∈(
,1),所以k(x)>0.
所以结论得证.…(14分)
点评:本题主要考查利用导数研究函数的有关性质,判断函数的单调性、求函数的极值、最值等知识,考查学生分析问题、解决问题的能力及运算求解能力,属于难题.



 黄冈创优卷系列答案
黄冈创优卷系列答案 如图,在四棱椎P-ABCD中,PD⊥平面ABCD,CD∥AB,CD⊥DA且PD=DA=AB=
如图,在四棱椎P-ABCD中,PD⊥平面ABCD,CD∥AB,CD⊥DA且PD=DA=AB=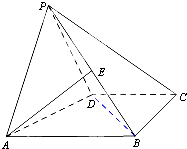 如图,在四棱锥P-ABCD中,已知侧面PAD为等腰直角三角形,底面ABCD为直角梯形,AB∥CD,∠ABC=∠APD=90°,侧面PAD⊥底面ABCD,且AB=4,AP=PD=BC=CD=2.
如图,在四棱锥P-ABCD中,已知侧面PAD为等腰直角三角形,底面ABCD为直角梯形,AB∥CD,∠ABC=∠APD=90°,侧面PAD⊥底面ABCD,且AB=4,AP=PD=BC=CD=2.