
如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,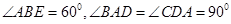 ,点H、G分别是线段EF、BC的中点.
,点H、G分别是线段EF、BC的中点.
(1)求证:平面AHC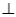 平面
平面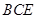 ;(2)(2)求此几何体的体积.
;(2)(2)求此几何体的体积.
(1)详见解析;(2)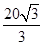 .
.
解析试题分析:(1)要证面面垂直,首先证线面垂直.那么在本题中证哪条线垂直哪个面?结合条件可得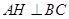 ,
,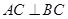 ,所以
,所以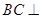 面AHC,从而平面AHC
面AHC,从而平面AHC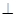 平面BCE.(2)可将该几何体切割为三部分:
平面BCE.(2)可将该几何体切割为三部分: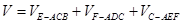 ,然后分别求出三部分的体积相加即得.
,然后分别求出三部分的体积相加即得.
(1)在菱形ABEF中,因为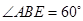 ,所以
,所以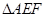 是等边三角形,又因为H是线段EF的中点,所以
是等边三角形,又因为H是线段EF的中点,所以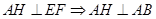
因为面ABEF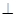 面ABCD,且面ABEF
面ABCD,且面ABEF 面ABCD=AB,
面ABCD=AB,
所以AH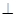 面ABCD,所以
面ABCD,所以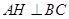
在直角梯形中,AB=2AD=2CD=4,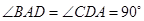 ,得到
,得到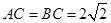 ,从而
,从而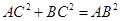 ,所以
,所以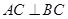 ,又AH
,又AH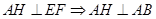 AC=A
AC=A
所以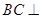 面AHC,又
面AHC,又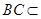 面BCE,所以平面AHC
面BCE,所以平面AHC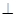 平面BCE .6分
平面BCE .6分
(2)因为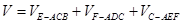 ,
,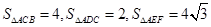
所以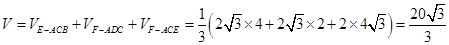 .12分
.12分
考点:(1)空间直线与平面的关系;(2)几何体的体积.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:解答题
如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2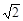 ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.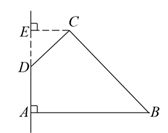
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图是某几何体的三视图,它的正视图和侧视图均为矩形,俯视图为正三角形(长度单位:cm)
(1)试说出该几何体是什么几何体;
(2)按实际尺寸画出该几何体的直观图,并求它的表面积及体积.(只要做出图形,不要求写作法)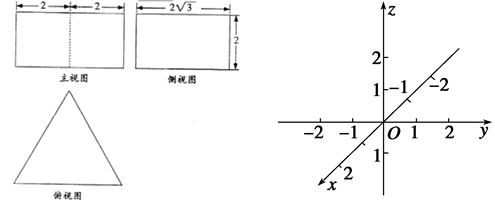
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知平面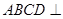 平面
平面 ,且四边形
,且四边形 为矩形,四边形
为矩形,四边形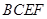 为直角梯形,
为直角梯形,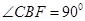 ,
,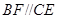 ,
,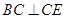 ,
,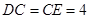 ,
,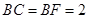 .
.
(1)作出这个几何体的三视图(不要求写作法).
(2)设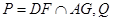 是直线
是直线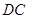 上的动点,判断并证明直线
上的动点,判断并证明直线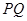 与直线
与直线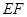 的位置关系.
的位置关系.
(3)求直线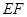 与平面
与平面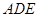 所成角的余弦值.
所成角的余弦值.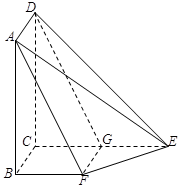
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知一个几何体的三视图如图所示.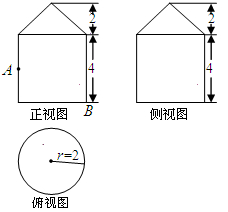
(1)求此几何体的表面积;
(2)在如图的正视图中,如果点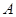 为所在线段中点,点
为所在线段中点,点 为顶点,求在几何体侧面上从点
为顶点,求在几何体侧面上从点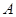 到点
到点 的最短路径的长.
的最短路径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com