
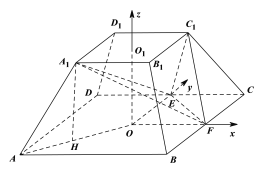
【题目】用一个平行于底面的截面去截一个正棱锥,截面和底面间的几何体叫正棱台.如图,在四棱台![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() 的中点.
的中点.
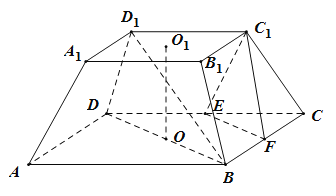
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若侧棱所在直线与上下底面中心的连线![]() 所成的角为
所成的角为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成的角的余弦值.
所成的角的余弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,由已知
,由已知![]() ,证得四边形
,证得四边形![]() 是平行四边形,即
是平行四边形,即![]() 是
是![]() 的中点,再由三角形的中位线定理证得
的中点,再由三角形的中位线定理证得![]() ,最后由线面平行的判定定理得证;
,最后由线面平行的判定定理得证;
(Ⅱ)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,由已知关系分别表示
轴,由已知关系分别表示![]() 的坐标,进而表示
的坐标,进而表示![]() 与平面
与平面![]() 的法向量
的法向量![]() ,最后由空间向量求线面角的运算公式求得答案即可.
,最后由空间向量求线面角的运算公式求得答案即可.
(Ⅰ)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,
,
在正四棱台![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() 的中点
的中点
所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() 是
是![]() 的中点.
的中点.
因为![]() 是
是![]() 的中点,所以
的中点,所以![]() 是
是![]() 的中位线.
的中位线.
所以![]() ,且
,且![]() 面
面![]() ,
,
故![]() 平面
平面![]() .
.
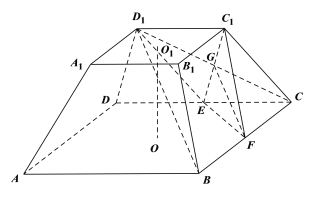
(Ⅱ)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,
![]() 为
为![]() 轴,建立空间直角坐标系.不妨设
轴,建立空间直角坐标系.不妨设![]() ,
,
过![]() 做
做![]() 于
于![]() ,
,![]() 平面
平面![]()
则![]() 为测棱与底面所成的角,即
为测棱与底面所成的角,即![]() ,
,
![]() ,所以
,所以![]() ,
,![]() ,
,
![]() ,
,![]() ,则
,则![]() ,
,![]()
设平面![]() 的法向量
的法向量![]()
则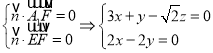 ,
,
令![]() ,则
,则![]() ,
,![]()
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
所以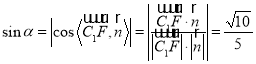 ,
,
![]() ,
,
故直线![]() 与平面
与平面![]() 所成的角的余弦值为
所成的角的余弦值为![]() .
. 


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求直线
,求直线![]() 与曲线
与曲线![]() 的交点的直角坐标;
的交点的直角坐标;
(2)若点![]() 在曲线
在曲线![]() 上,且
上,且![]() 到直线
到直线![]() 距离的最大值为
距离的最大值为![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在市中心有一矩形空地![]() .市政府欲将它改造成绿化景观带,具体方案如下:在边
.市政府欲将它改造成绿化景观带,具体方案如下:在边![]() 上分别取点M,N,在三角形
上分别取点M,N,在三角形![]() 内建造假山,在以
内建造假山,在以![]() 为直径的半圆内建造喷泉,其余区域栽种各种观赏类植物.
为直径的半圆内建造喷泉,其余区域栽种各种观赏类植物.
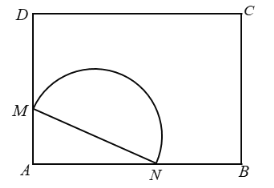
(1)若假山区域面积为![]() ,求喷泉区域面积的最小值;
,求喷泉区域面积的最小值;
(2)若![]() ,求假山区域面积的最大值.
,求假山区域面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
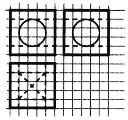
【题目】某石雕构件的三视图如图所示,该石雕构件最中间的镂空部分是一个独特的几何体——牟合方盖(在一个立方体内作两个互相垂直的内切圆柱,其相交的部分),其体积![]() (其中
(其中![]() 为最大截面圆的直径).若三视图中网格纸上小正方形的边长为1,则该石雕构件的体积为( )
为最大截面圆的直径).若三视图中网格纸上小正方形的边长为1,则该石雕构件的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解户籍、性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为200的调查样本,其中城镇户籍与农村户籍各100人;男性120人,女性80人,绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图,如图所示,其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
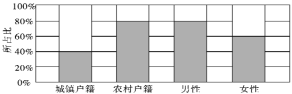
A. 是否倾向选择生育二胎与户籍有关
B. 是否倾向选择生育二胎与性别有关
C. 倾向选择生育二胎的人群中,男性人数与女性人数相同
D. 倾向选择不生育二胎的人群中,农村户籍人数少于城镇户籍人数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把方程![]() 表示的曲线作为函数
表示的曲线作为函数![]() 的图象,则下列结论正确的是( )
的图象,则下列结论正确的是( )
①![]() 在R上单调递减
在R上单调递减
②![]() 的图像关于原点对称
的图像关于原点对称
③![]() 的图象上的点到坐标原点的距离的最小值为3
的图象上的点到坐标原点的距离的最小值为3
④函数![]() 不存在零点
不存在零点
A.①③B.①②③C.①③④D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在
,若存在![]() ,使
,使![]() 恒成立,则称
恒成立,则称![]() 为“
为“![]() 型函数”;若存在
型函数”;若存在![]() ,使
,使![]() 恒成立,则称
恒成立,则称![]() 为“
为“![]() 型函数”.已知函数
型函数”.已知函数![]() .
.
(1)设函数![]() .若
.若![]() ,且
,且![]() 为“
为“![]() 型函数”,求
型函数”,求![]() 的取值范围;
的取值范围;
(2)设函数![]() .证明:当
.证明:当![]() ,
,![]() 为“
为“![]() (1)型函数”;
(1)型函数”;
(3)若![]() ,证明存在唯一整数
,证明存在唯一整数![]() ,使得
,使得![]() 为“
为“![]() 型函数”.
型函数”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图像向左平移
的图像向左平移![]() 个单位后得到函数
个单位后得到函数![]() 的图像,且函数
的图像,且函数![]() 满足
满足![]() ,则下列命题中正确的是()
,则下列命题中正确的是()
A. 函数![]() 图像的两条相邻对称轴之间的距离为
图像的两条相邻对称轴之间的距离为![]()
B. 函数![]() 图像关于点
图像关于点![]() 对称
对称
C. 函数![]() 图像关于直线
图像关于直线![]() 对称
对称
D. 函数![]() 在区间
在区间![]() 内为单调递减函数
内为单调递减函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com