
分析 (1)把k=2代入不等式组,画出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求出最优解的坐标,代入目标函数求得x+2y的最大值;
(2)由题意可知,当k=0时可行域为直线;当k≠0时,通过把可行域变形,得到正方形区域求整点个数.
解答 解:(1)当k=2时,不等式组为$\left\{\begin{array}{l}{y≥0}\\{y≤4}\\{2x-y≥0}\\{2x-y-8≤0}\end{array}\right.$,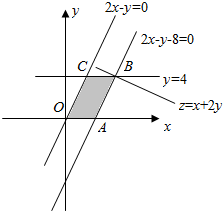
对应的平面区域如图,
联立$\left\{\begin{array}{l}{y=4}\\{2x-y-8=0}\end{array}\right.$,解得B(6,4),
令z=x+2y,化为y=-$\frac{x}{2}+\frac{z}{2}$,
由图可知,当直线y=-$\frac{x}{2}+\frac{z}{2}$过B时,直线在y轴上的截距最大,z有最大值为6+2×4=14.
∴x+2y的最大值为14;
(2)由题意,当k=0时,原不等式化为$\left\{\begin{array}{l}{y≥0}\\{y≤4}\\{y≤0}\end{array}\right.$,即y=0,平面区域为直线y=0,区域W内部的整点的个数有无数个;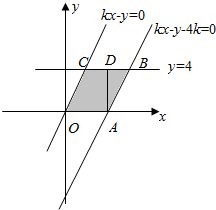
当k≠0时,不等式组$\left\{\begin{array}{l}{y≥0}\\{y≤4}\\{kx-y≥0}\\{kx-y-4k≤0}\end{array}\right.$表示的平面区域W如图,
${x}_{C}=\frac{4}{k}$,${x}_{B}=\frac{4}{k}+4$,则BC长度为4.
当OC过整点个数分别为1、2、3、4、5时,区域W内部的整点的个数分别为:21、22、23、24、25.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,(2)中改变可行域形状求整点是该题的难点,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10250 | B. | 3430 | C. | 825 | D. | 405 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 4 | C. | -6或4 | D. | 6或4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
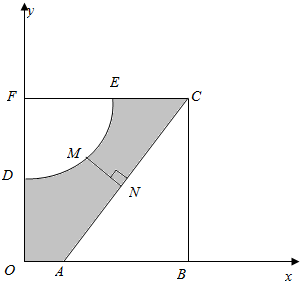 如图,河的两岸,分别有生活小区ABC和DEF,其中AB⊥BC,EF⊥DF,DF⊥AB,C,E,F三点共线,FD与BA的延长线交于点O,测得AB=3km,BC=4km,DF=$\frac{9}{4}$km,FE=3km,EC=$\frac{3}{2}$km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y=$\frac{x+b}{x+a}$(其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分.
如图,河的两岸,分别有生活小区ABC和DEF,其中AB⊥BC,EF⊥DF,DF⊥AB,C,E,F三点共线,FD与BA的延长线交于点O,测得AB=3km,BC=4km,DF=$\frac{9}{4}$km,FE=3km,EC=$\frac{3}{2}$km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y=$\frac{x+b}{x+a}$(其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com