
【题目】已知函数![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() ,
,![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)答案见解析;(2)![]() .
.
【解析】试题分析:(1)对函数求导研究函数的单调性,通过导函数的正负得到原函数的单调区间;(2)![]() 对任意
对任意![]() 恒成立,即
恒成立,即![]() 对任意
对任意![]() 恒成立,令
恒成立,令![]() ,对这个函数求导研究函数的单调性,使得最值大于0即可.
,对这个函数求导研究函数的单调性,使得最值大于0即可.
解析;
(1)![]() ,定义域
,定义域![]()
所以![]() .
.
讨论:
当![]() 时,对
时,对![]() 或
或![]() ,
,![]() 成立,
成立,
所以函数![]() 在区间
在区间![]() ,
,![]() 上均是单调递增;
上均是单调递增;
当![]() 时,对
时,对![]() 或
或![]() ,
,![]() 成立,
成立,
所以函数![]() 在区间
在区间![]() ,
,![]() 上均是单调递减;
上均是单调递减;
当![]() 时,函数
时,函数![]() 是常函数,无单调性.
是常函数,无单调性.
(2)若![]() ,
,![]() 对任意
对任意![]() 恒成立,即
恒成立,即![]() 对任意
对任意![]() 恒成立.
恒成立.
令![]() ,则
,则![]() .
.
讨论:
①当![]() ,即
,即![]() 时,
时,![]() 且
且![]() 不恒为0,
不恒为0,
所以函数![]() 在区间
在区间![]() 单调递增.
单调递增.
又![]() ,所以
,所以![]() 对任意
对任意![]() 恒成立.
恒成立.
故![]() 符合题意
符合题意
②当![]() 时,令
时,令![]() 得
得![]() ;令
;令![]() ,得
,得![]() .
.
所以函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
所以![]() ,即当
,即当![]() 时,存在
时,存在![]() ,使
,使![]() .
.
故知![]() 对任意
对任意![]() 不恒成立,故
不恒成立,故![]() 不符合题意.
不符合题意.
综上实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
该社团将该校区在2018年11月中10天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.

(Ⅰ)以这10天的空气质量指数监测数据作为估计2018年11月的空气质量情况,则2018年11月中有多少天的空气质量达到优良?
(Ⅱ)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化空气的费用为1000元,空气质量等量等级为3级时每天需净化空气的费用为2000元.若从这10天样本中空气质量为1级、2级、3级的天数中任意抽取两天,求这两天的净化空气总费用为3000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品价格与该商品日需求量之间的几组对照数据如下表:
![]()
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归方程,当价格x=40元/kg时,日需求量y的预测值为多少?
参考公式:线性回归方程![]() ,其中
,其中![]() =
=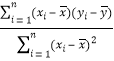 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn,若S9=81,a3+a5=14.
(1)求数列{an}的通项公式;
(2)设bn=![]() ,若{bn}的前n项和为Tn,证明:Tn<
,若{bn}的前n项和为Tn,证明:Tn<![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在航天员进行的一项太空实验中,要先后实施6个程序,其中程序![]() 只能出现在第一步或最后一步,程序
只能出现在第一步或最后一步,程序![]() 实施时必须相邻,请问实验顺序的编排方法共有 ( )
实施时必须相邻,请问实验顺序的编排方法共有 ( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式e2x﹣alnx![]() a恒成立,则实数a的取值范围是( )
a恒成立,则实数a的取值范围是( )
A.[0,2e]B.(﹣∞,2e]C.[0,2e2]D.(﹣∞,2e2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,交圆
两点,交圆![]() 于
于![]() 两点(
两点(![]() 两点相邻).
两点相邻).
(Ⅰ)若![]() ,当
,当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(Ⅱ)过![]() 两点分别作曲线
两点分别作曲线![]() 的切线
的切线![]() ,两切线交于点
,两切线交于点![]() ,求
,求![]() 与
与![]() 面积之积的最小值.
面积之积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某船在海面![]() 处测得灯塔
处测得灯塔![]() 在北偏东
在北偏东![]() 方向,与
方向,与![]() 相距
相距![]() 海里,测得灯塔
海里,测得灯塔![]() 在北偏西
在北偏西![]() 方向,与
方向,与![]() 相距
相距![]() 海里,船由
海里,船由![]() 向正北方向航行到
向正北方向航行到![]() 处,测得灯塔
处,测得灯塔![]() 在南偏西
在南偏西![]() 方向,这时灯塔
方向,这时灯塔![]() 与
与![]() 相距多少海里?
相距多少海里?![]() 在
在![]() 的什么方向?
的什么方向?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() :
:![]() ,直线
,直线![]() :
:![]() .以极点
.以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的正半轴建立平面直角坐标系.
轴的正半轴建立平面直角坐标系.
(1)求直线![]() ,
,![]() 的直角坐标方程以及曲线
的直角坐标方程以及曲线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com