练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数是定义域为R的奇函数， .

    (Ⅰ)若，求m的取值范围；

    (Ⅱ)若在上的最小值为-2，求m的值.

    【答案】(1) 或.（2）m=2

    【解析】试题分析：（1）先由奇函数确定k，再由解得a=2，进而确定单调性，最后根据单调性化简函数不等式为一元二次不等式，解得m的取值范围；（2）令，则函数转化为二次函数，根据对称轴与定义区间位置关系讨论最值取法，进而确定m的值.

    试题解析：解：（Ⅰ）由题意，得，即k-1=0，解得k=1

    由，得，解得a=2， （舍去）

    所以为奇函数且是R上的单调递增函数.

    由，得

    所以，解得或.

    (Ⅱ)

    令，由 所以

    所以，对称轴t=m

    (1) 时， ，解得m=2

    (2) 时， （舍去）

    所以m=2

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数

    (1)求函数的最大值；

    (2)令既有极大值，又有极小值，求实数a的范围；

    (3)求证：当以．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ．

    （Ⅰ）当时，求曲线在点处的切线方程．

    （Ⅱ）当时，若曲线上的点都在不等式组所表示的平面区域内，试求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以A表示值域为R的函数组成的集合,B表示具有如下性质的函数组成的集合:对于函数,存在一个正数M,使得函数的值域包含于区间.例如,当时, . 现有如下命题:

    ①设函数的定义域为D,则“”的充要条件是“”;

    ②若函数,则有最大值和最小值;

    ③若函数的定义域相同,且,则;

    ④若函数有最大值,则.

    其中的真命题有___________. (写出所有真命题的序号)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高校在2017年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如下左图所示。

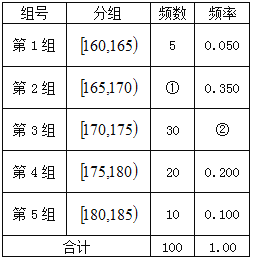
    （1）请先求出频率分布表中①、②位置相应数据，再在答题纸上完成下列频率分布直方图；

    （2）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试？

    （3）在（2）的前提下，学校决定在6名学生中随机抽取2名学生接受A教官进行面试，求：第4组至少有一名学生被考官A面试的概率？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市垃圾处理站每月的垃圾处理成本（元）与月垃圾处理量（吨）之间的函数关系可近似地表示为，求该站每月垃圾处理量为多少吨时，才能使每吨垃圾的平均处理成本最低？最低平均处理成本是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

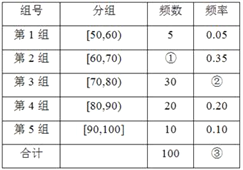
    【题目】某校随机抽取100名学生高中学业水平考试的X科成绩，并将成绩分成5组，得到频率分布表(部分)如下．

    (1)直接写出频率分布表中①②③的值；

    (2)如果每组学生的平均分都是分组端点的平均值(例如，第1组5个学生的平均分是＝55)，估计该校学生本次学业水平测试X科的平均分.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）当时，若函数存在零点，求实数的取值范围；

    （Ⅱ）若恒成立，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列，其前项和为.

    （1）若对任意的， ， ， 组成公差为4的等差数列，且，求；

    （2）若数列是公比为（）的等比数列， 为常数，

    求证：数列为等比数列的充要条件为.

    查看答案和解析>>

    同步练习册答案