
【题目】已知命题![]() ,
,![]() ;命题
;命题![]() 关于
关于![]() 的方程
的方程![]() 有两个相异实数根.
有两个相异实数根.
(1)若![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 为真命题,
为真命题,![]() 为假命题,求实数
为假命题,求实数![]() 的取值范围.
的取值范围.
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】班级新年晚会设置抽奖环节.不透明纸箱中有大小相同的红球3个,黄球2个,且这5个球外别标有数字1、2、3、4、5.有如下两种方案可供选择:
方案一:一次性抽取两球,若颜色相同,则获得奖品;
方案二:依次有放回地抽取两球,若数字之和大于5,则获得奖品.
(1)写出按方案一抽奖的试验的所有基本事件;
(2)哪种方案获得奖品的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,已知椭圆![]() 经过点
经过点![]() ,且其左右焦点的坐标分别是
,且其左右焦点的坐标分别是![]() ,
,![]() .
.
(1)求椭圆![]() 的离心率及标准方程;
的离心率及标准方程;
(2)设![]() 为动点,其中
为动点,其中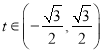 ,直线
,直线![]() 经过点
经过点![]() 且与椭圆
且与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() 为
为![]() 的中点,是否存在定点
的中点,是否存在定点![]() ,使
,使![]() 恒成立?若存在,求点
恒成立?若存在,求点![]() 的坐标;若不存在,说明理由
的坐标;若不存在,说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y),f(2)=1.
(1)求f(8)的值;
(2)求不等式f(x)-f(x-2)>3的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
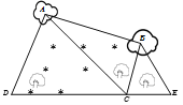
【题目】如图,为了测量某湿地![]() 两点间的距离,观察者找到在同一直线上的三点
两点间的距离,观察者找到在同一直线上的三点![]() .从
.从![]() 点测得
点测得![]() ,从
,从![]() 点测得
点测得![]() ,
,![]() ,从
,从![]() 点测得
点测得![]() .若测得
.若测得![]() ,
,![]() (单位:百米),则
(单位:百米),则![]() 两点的距离为( )
两点的距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,ABCD为梯形,AB//CD,BC⊥AB,AB=2![]() ,BC=
,BC=![]() ,CD=PC=
,CD=PC=![]() 。
。
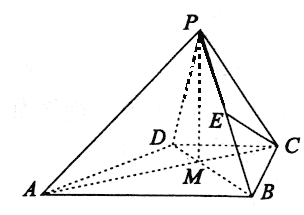
(I)点E在线段PB上,满足CE//平面PAD,求![]() 的值。
的值。
(II)已知AC与BD的交点为M,若PM=1,且平面PAC⊥平面ABCD,求二面角P-BC-M平面角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上.圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0).
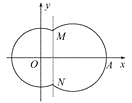
(1)求圆弧C2的方程.
(2)曲线C上是否存在点P,满足PA=![]() PO?若存在,指出有几个这样的点;若不存在,请说明理由.
PO?若存在,指出有几个这样的点;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂修建一个长方体无盖蓄水池,其容积为6400立方米,深度为4米.池底每平方米的造价为120元,池壁每平方米的造价为100元.设池底长方形的长为x米.
(Ⅰ)求底面积,并用含x的表达式表示池壁面积;
(Ⅱ)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com