
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
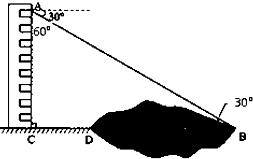 如图,某同学在楼房的A处测得荷塘的一端B处的俯角为30°,荷塘另一端D处与C、B在同一条直线上,已知AC=32米,CD=16米,求荷塘宽BD为多少米?(取
如图,某同学在楼房的A处测得荷塘的一端B处的俯角为30°,荷塘另一端D处与C、B在同一条直线上,已知AC=32米,CD=16米,求荷塘宽BD为多少米?(取| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山西省高三9月月考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)在某学校组织的一次篮球定点投篮训练中,规定每人最多投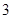 次:在
次:在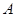 处每投进一球得
处每投进一球得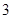 分,在
分,在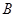 处每投进一球得
处每投进一球得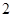 分;如果前两次得分之和超过
分;如果前两次得分之和超过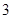 分即停止投篮,否则投第三次.某同学在
分即停止投篮,否则投第三次.某同学在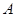 处的命中率
处的命中率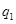 为
为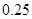 ,在
,在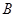 处的命中率为
处的命中率为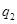 ,该同学选择先在
,该同学选择先在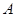 处投一球,以后都在
处投一球,以后都在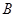 处投,用
处投,用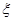 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
|
|
0 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
(1) 求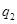 的值;
的值; (2)
求随机变量
(2)
求随机变量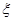 的数学期望
的数学期望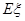 ;
;
(3) 试比较该同学选择都在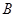 处投篮得分超过
处投篮得分超过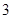 分与选择上述方式投篮得分超过
分与选择上述方式投篮得分超过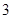 分的概率的大小.
分的概率的大小.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市高三第二次月考理科数学卷 题型:解答题
(本小题满分13分)在某校组织的一次篮球定点投篮训练中,规定每人最多投 次;在
次;在 处每投进一球得
处每投进一球得 分,在
分,在 处每投进一球得
处每投进一球得 分;如果前两次得分之和超过
分;如果前两次得分之和超过 分即停止投篮,否则投第三次,某同学在
分即停止投篮,否则投第三次,某同学在 处的命中率
处的命中率 为
为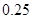 ,在
,在 处的命中率为
处的命中率为 ,该同学选择先在
,该同学选择先在 处投一球,以后都在
处投一球,以后都在 处投,用
处投,用 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
|
|
0 |
2 |
3 |
4 |
5 |
|
p |
0.03 |
P1 |
P2 |
P3 |
P4 |
(1)求 的值;
的值;
(2)求随机变量 的数学期望E
的数学期望E .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com