
| CB |
| e1 |
| CA |
| e2 |
| CF |
| 3 |
| 4 |
科目:高中数学 来源: 题型:
| x |
| 2 |
| π |
| 12 |
| 3 |
| x |
| 2 |
| π |
| 12 |
| x |
| 2 |
| π |
| 12 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
D、H、G为垂足.若将正△ABC绕AD旋转一周所得的圆锥体积为V,则其中由阴影部分所产生的旋转体的体积与V的比值为多少?

图6
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州四中高一(下)第一次质量检测数学试卷(解析版) 题型:填空题
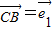 ,
,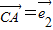 为基底时,向量
为基底时,向量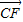 = ;函数
= ;函数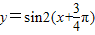 的奇偶性为 .
的奇偶性为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com