
【题目】某工厂生产甲、乙两种产品.已知生产一吨甲产品、一吨乙产品所需要的煤、电以及产值如表所示;又知道国家每天分配给该厂的煤和电力有限制,每天供煤至多56吨,供电至多45千瓦.问该厂如何安排生产,才能使该厂日产值最大?最大的产值是多少?
用煤(吨) | 用电(千瓦) | 产值(万元) | |
生产一吨 甲种产品 | 7 | 2 | 8 |
生产一吨 乙种产品 | 3 | 5 | 11 |
【答案】该厂每天生产甲种产品5吨,乙种产品7吨,能使该厂日产值最大,最大的产值是117万元.
【解析】试题分析:
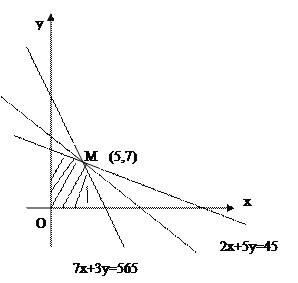
该问题考查线性规划的实际应用,由题意建立数学模型,每天生产甲种产品x吨,乙种产品y吨, 列出约束条件,且目标函数为![]() ,结合目标函数的几何意义可得当
,结合目标函数的几何意义可得当![]() 时,
时, ![]() ,即该厂每天生产甲种产品5吨,乙种产品7吨,能使该厂日产值最大,最大的产值是117万元.
,即该厂每天生产甲种产品5吨,乙种产品7吨,能使该厂日产值最大,最大的产值是117万元.
试题解析:
设每天生产甲种产品x吨,
乙种产品y吨, 可得线性约束条件
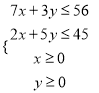
目标函数为 ![]() ,
,
作出线性约束条件所表示的平面区域,
如图所示:
将![]() 变形为
变形为![]()
当直线![]() 在纵轴上的截距
在纵轴上的截距![]() 达到最大值时,
达到最大值时, ![]() 取最大值.
取最大值.
从图中可知,当直线![]() 经过点M时,
经过点M时, ![]() 达到最大值.
达到最大值.
由![]() 得M点的坐标为(5,7)
得M点的坐标为(5,7)
所以当![]() 时,
时, ![]()
因此,该厂每天生产甲种产品5吨,乙种产品7吨,能使该厂日产值最大,最大的产值是117万元.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】已知三条直线l1:2x-y+a=0(a>0),直线l2:4x-2y-1=0和直线l3:x+y-1=0,且l1和l2的距离是![]() .
.
(1)求a的值.
(2)能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到l1的距离是P点到l2的距离的![]() ;③P点到l1的距离与P点到l3的距离之比是
;③P点到l1的距离与P点到l3的距离之比是![]() ?若能,求出P点坐标;若不能,请说明理由.
?若能,求出P点坐标;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点的椭圆![]() 的长轴的一个端点是抛物线
的长轴的一个端点是抛物线![]() 的焦点,且椭圆
的焦点,且椭圆![]() 的离心率是
的离心率是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的动直线与椭圆
的动直线与椭圆![]() 相交于
相交于![]() 两点.若线段
两点.若线段![]() 的中点的横坐标是
的中点的横坐标是![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本为
千件,需另投入成本为![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元).当年产量不小于80千件时
(万元).当年产量不小于80千件时![]() (万元).每件商品售价为0.05万元.通过分析,该工厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过分析,该工厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某物流公司购买了一块长AM=30米,宽AN=20米的矩形地块,计划把图中矩形ABCD建设为仓库,其余地方为道路和停车场,要求顶点C在地块对角线MN上,B、D分别在边AM、AN上,假设AB的长度为x米
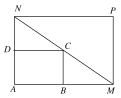
(1)求矩形ABCD的面积S关于x的函数解析式;
(2)要使仓库占地ABCD的面积不少于144平方米,则AB的长度应在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,函数g(x)=f(x)﹣k.
,函数g(x)=f(x)﹣k.
(1)当m=2时,若函数g(x)有两个零点,则k的取值范围是;
(2)若存在实数k使得函数g(x)有两个零点,则m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等差数列,{bn}是等比数列,其中a1=b1=1,a2≠b2,且b2为a1、a2的等差中项,a2为b2、b3的等差中项.
(1)求数列{an}与{bn}的通项公式;
(2)记![]() ,求数列{cn}的前n项和Sn.
,求数列{cn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,过椭圆C的右焦点且垂直于x轴的直线与椭圆交于A,B两点,且|AB|=
,过椭圆C的右焦点且垂直于x轴的直线与椭圆交于A,B两点,且|AB|= ![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点(1,0)的直线l交椭圆C于E,F两点,若存在点G(﹣1,y0)使△EFG为等边三角形,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com