
����Ŀ��ijСѧ�����꼶��ѧ���������ʲ��ԣ���֪����һ���ѧ��30�ˣ�����������Զ�ijɼ��þ�Ҷͼ��ʾ��ͼ����λ��cm���� �����ɼ���175cm���ϣ�����175cm������Ϊ���ϸ��ɼ���175cm���£�������175cm������Ϊ�����ϸ�
Ů���ɼ���165cm���ϣ�����165cm������Ϊ���ϸ��ɼ���165cm���£�������165cm������Ϊ�����ϸ�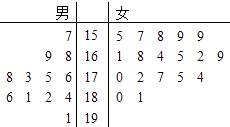
��1��������һ���Ů��������Զ�ɼ�����λ����
��2��������һ�������������ѡȡ3�ˣ���������2�˵ijɼ��Ǻϸ�ĸ��ʣ�
��3����������һ��ɼ����ϸ�ѧ����ѡȡ2�˲μӸ��ԣ���X��ʾ����������������д��X�ķֲ��У�����X����ѧ������
���𰸡�
��1���⣺�ɾ�Ҷͼ������һ���Ů��������Զ�ɼ�����λ��Ϊ ![]() cm��
cm��
��2���⣺�衰�������˵ijɼ��ϸ�Ϊ�¼�A���������˵ijɼ��ϸ�Ϊ�¼�B��
���������˵ijɼ��Ǻϸ�ĸ��ʣ�P=P��A��+P��B����
��������12�ˣ�������8�˺ϸӶ� ![]() ��
��
![]() ������
������ ![]() ��
��
��3���⣺��ΪŮ������18�ˣ�������10�˺ϸ�
�����⣬X��ȡֵΪ0��1��2��
�� ![]() ��
��
![]() ��
��
![]() ��
��
��ˣ�X�ķֲ������£�
X | 0 | 1 | 2 |
P |
|
|
|
�� ![]() ���ˣ���
���ˣ���
�����ǣ���ΪX���ӳ����ηֲ������� ![]() ���ˣ�
���ˣ�
����������1���ɾ�Ҷͼ���������һ���Ů��������Զ�ɼ�����λ������2���衰�������˵ijɼ��ϸ�Ϊ�¼�A���������˵ijɼ��ϸ�Ϊ�¼�B�����������˵ijɼ��Ǻϸ�ĸ��ʣ�P=P��A��+P��B�����ɴ������������2�˵ijɼ��Ǻϸ�ĸ��ʣ���3����ΪŮ������18�ˣ�������10�˺ϸ������⣬X��ȡֵΪ0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�X����ѧ������
�����㾫����ͨ��������þ�Ҷͼ��ƽ��������λ�������������վ�Ҷͼ�ֳơ�֦Ҷͼ��������˼·�ǽ������е�����λ�����бȽϣ������Ĵ�С���������仯�����λ��Ϊһ�����ɣ����������仯���λ������Ϊ��֦��Ҷ�����������ɵĺ��棬�����Ϳ�������ؿ���ÿ�����ɺ���ļ�������ÿ���������Ƕ��٣���ƽ��������������λ����������һ�����ݼ������Ƶ�������ƽ��������������λ�����е�λ����ƽ������ӳһ�����ݵ�ƽ��ˮƽ�������������е�ÿ�������й�ϵ��������Ϊ��Ҫ��Ӧ����㣻����λ�����ܸ���ƫ���ƫС���ݵ�Ӱ�죻��������������ݳ��ֵ�Ƶ���йأ����ܸ������ݵ�Ӱ�죬��ʱ��������Ϊ���ĵ����ݼ����Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ABC���ڽ�A��B��C���Աߵij��ֱ�Ϊa��b��c�����������⣺
����ab��c2 �� ��C ![]() ��
��
����a+b��2c����C ![]() ��
��
����a3+b3=c3 �� ��C ![]() ��
��
������a+b��c��2ab����ab��c2��
������a2+b2��c2��2a2b2 �� ��C ![]() ��
��
������ȷ��������д��������ȷ�������ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪������ABCD��A1B1C1D1�У�AB=BC=2��AA1=4��E����CC1�ϵĵ㣬��BE��B1C�� 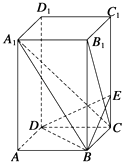
��1����CE�ij���
��2����֤��A1C��ƽ��BED��
��3����A1B��ƽ��BDE�нǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��F��x��= ![]() ������f��x��=log2��x2+1����g��x��=log2��|x|+7����
������f��x��=log2��x2+1����g��x��=log2��|x|+7����
��1����ʵ����R���÷ֶκ�����ʽд������F��x���Ľ���ʽ��
��2������F��x������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��֤���뻯��
��1����֤��cot��=tan��+2cot2����
��2�������ã�1���Ľ���֤����cot��=tan��+2tan2��+4cot4����
��3������ѣ�2���Ľ����Ƶ���һ������Σ�ʹ֮��Ϊ�ƹ���������������֤����
��4������tan5��+2tan10��+4tan20��+8tan50�㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() =1��a��b��0����������Ϊ
=1��a��b��0����������Ϊ ![]() ����ԭ��ΪԲ�ģ���Բ�Ķ̰���Ϊ�뾶��Բ��ֱ��x��y+
����ԭ��ΪԲ�ģ���Բ�Ķ̰���Ϊ�뾶��Բ��ֱ��x��y+ ![]() =0���У�����P��4��0���Ҳ���ֱ��x��ֱ��l����ԲC�ཻ��A��B���㣮
=0���У�����P��4��0���Ҳ���ֱ��x��ֱ��l����ԲC�ཻ��A��B���㣮
��1������ԲC�ķ��̣�
��2���� ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����B�����x��ĶԳƵ���E��֤����ֱ��AE��x���ཻ�ڶ��㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ���ռ伸���������ͼ��ͼ��ʾ������ͼ�б���ijߴ磬�ɵ�����������ȫ���Ϊ�� �� 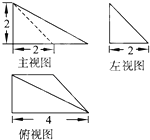
A.10+4 ![]() ?+4
?+4 ![]()
B.10+2 ![]() ?+4
?+4 ![]() ??
??
C.14+2 ![]() ?+4
?+4 ![]()
D.14+4 ![]() ?+4
?+4 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����0��x1��x2��1���� ��
A.![]() ��
�� ![]() ��lnx2��lnx1
��lnx2��lnx1
B.![]() ��
�� ![]() ��lnx2��lnx1
��lnx2��lnx1
C.x2 ![]() ��x1
��x1 ![]()
D.x2 ![]() ��x1
��x1 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������R�ϵ�ż����f��x���ڣ�0��+�ޣ���������������f�� ![]() ��=0����ʽxf��x����0�Ľ⼯�ǣ� ��
��=0����ʽxf��x����0�Ľ⼯�ǣ� ��
A.��0�� ![]() ��
��
B.�� ![]() ��+�ޣ�??
��+�ޣ�??
C.���� ![]() ��0���ȣ�
��0���ȣ� ![]() ��+�ޣ�
��+�ޣ�
D.�����ޣ��� ![]() ���ȣ�0��
���ȣ�0�� ![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com