
【题目】已知函数![]() 的定义域为区间
的定义域为区间![]() ,若对于
,若对于![]() 内任意
内任意![]() ,都有
,都有![]()
![]() 成立,则称函数
成立,则称函数![]() 是区间
是区间![]() 的“
的“![]() 函数”.
函数”.
(1)判断函数![]() (
(![]() )是否是“
)是否是“![]() 函数”?说明理由;
函数”?说明理由;
(2)已知![]() ,求证:函数
,求证:函数![]() (
(![]() )是“
)是“![]() 函数”;
函数”;
(3)设函数![]() 是
是![]() ,(
,(![]() )上的“
)上的“![]() 函数”,
函数”,![]() ,且存在
,且存在![]() 使得
使得![]() ,试探讨函数
,试探讨函数![]() 在区间
在区间![]() 上零点个数,并用图象作出简要的说明(结果不需要证明).
上零点个数,并用图象作出简要的说明(结果不需要证明).
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】阿基米德(公元前287年—公元前212年),伟大的古希腊哲学家、数学家和物理学家,他死后的墓碑上刻着一个“圆柱容球”的立体几何图形,为纪念他发现“圆柱内切球的体积是圆柱体积的![]() ,且球的表面积也是圆柱表面积的
,且球的表面积也是圆柱表面积的![]() ”这一完美的结论.已知某圆柱的轴截面为正方形,其表面积为
”这一完美的结论.已知某圆柱的轴截面为正方形,其表面积为![]() ,则该圆柱的内切球体积为( )
,则该圆柱的内切球体积为( )
A.![]() B.
B.![]() C.
C.![]()
![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() , 离心率为
, 离心率为![]() ,左右焦点分别为
,左右焦点分别为![]() , 过点
, 过点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点.
两点.
(1)求椭圆C的方程;
(2)当![]() 的面积为
的面积为![]() 时, 求以
时, 求以![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆的方程.
相切的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间在两天内,每天生产10件某产品,其中第一天第二天分别生产了1件2件次品,而质检部每天要在生产的10件产品中随意抽取4件进行检查,若发现有次品,则当天的产品不能通过.
(1)求两天全部通过检查的概率;
(2)若厂内对该车间生产的产品质量采用奖惩制度,两天全不通过检查罚300元,通过1天,2天分别奖300元900元.那么该车间在这两天内得到奖金的数学期望是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 是一个棱长为2的空心蔬菜大棚,由8个钢结构(地面没有)组合搭建而成的,四个侧面及顶上均被可采光的薄膜覆盖,已知
是一个棱长为2的空心蔬菜大棚,由8个钢结构(地面没有)组合搭建而成的,四个侧面及顶上均被可采光的薄膜覆盖,已知![]() 为柱
为柱![]() 上一点(不在点
上一点(不在点![]() 、
、![]() 处),
处),![]() (
(![]() ),菜农需要在地面正方形
),菜农需要在地面正方形![]() 内画出一条曲线
内画出一条曲线![]() 将菜地分隔为两个不同的区域来种植不同品种的蔬菜以加强管理,现已知点
将菜地分隔为两个不同的区域来种植不同品种的蔬菜以加强管理,现已知点![]() 为地面正方形
为地面正方形![]() 内的曲线
内的曲线![]() 上任意一点,设
上任意一点,设![]() 、
、![]() 分别为在
分别为在![]() 点处观测
点处观测![]() 和
和![]() 的仰角.
的仰角.
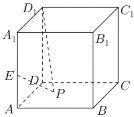
(1)若![]() ,请说明曲线
,请说明曲线![]() 是何种曲线,为什么?
是何种曲线,为什么?
(2)若![]() 为柱
为柱![]() 的中点,且
的中点,且![]() 时,请求出点
时,请求出点![]() 所在区域的面积.
所在区域的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com