
分析 (1)利用|EF|=2$\sqrt{2}$,建立方程,即可求E点的坐标.
(2)设直线PQ的方程为y=kx+b,通过直线PQ与已知圆相切,得到b2=2,通过求解$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0.证明PO⊥OQ.
(3)当直线ON垂直x轴时,直接求出O到直线MN的距离为$\frac{\sqrt{3}}{3}$.当直线ON不垂直x轴时,设直线ON的方程为:y=kx,(显然|k|>$\frac{\sqrt{2}}{2}$),推出直线OM的方程为y=-$\frac{1}{k}$x,求出|OM|2,|ON|2,设O到直线MN的距离为d,通过(|OM|2+|ON|2)d2=|OM|2|ON|2,求出d=$\frac{\sqrt{3}}{3}$.推出O到直线MN的距离是定值.
解答 (1)解:左焦点$F(-\frac{{\sqrt{6}}}{2},\;0)$.
设E(x,y),则$|EF{|^2}={(x+\frac{{\sqrt{6}}}{2})^2}+{y^2}={(\sqrt{3}x+\frac{{\sqrt{2}}}{2})^2}$,…(2分)
由E是右支上一点,知$x≥\frac{{\sqrt{2}}}{2}$,所以$|EF|=\sqrt{3}x+\frac{{\sqrt{2}}}{2}=2\sqrt{2}$,得$x=\frac{{\sqrt{6}}}{2}$.
所以$E(\frac{{\sqrt{6}}}{2},\;±\sqrt{2})$.…(4分)
(2)证明:设直线PQ的方程是y=x+b.因直线与已知圆相切,
故$\frac{|b|}{\sqrt{2}}$=1,即b=$\sqrt{2}$.…(6分)
由y=x+b与双曲线C1:2x2-y2=1联立,得x2-2bx-b2-1=0,
设P(x1,y1),Q(x2,y2),则x1+x2=2b,x1x2=-b2-1,
又y1y2=(x1+b)(x2+b).
所以$\overrightarrow{OP}$•$\overrightarrow{OQ}$=x1x2+y1y2=2x1x2+b(x1+x2)+b2
=2(-1-b2)+2b2+b2
=b2-2=0.
故PO⊥OQ.…(10分)
(3)当直线ON垂直于x轴时,
|ON|=1,|OM|=$\frac{\sqrt{2}}{2}$,则O到直线MN的距离为$\frac{\sqrt{3}}{3}$.
当直线ON不垂直于x轴时,
设直线ON的方程为y=kx(显然|k|>$\frac{\sqrt{2}}{2}$),则直线OM的方程为y=-$\frac{1}{k}$x.
由y=kx与椭圆方程联立,得x2=$\frac{1}{4+{k}^{2}}$,y2=$\frac{{k}^{2}}{4+{k}^{2}}$,所以|ON|2=$\frac{1+{k}^{2}}{4+{k}^{2}}$.
同理|OM|2=$\frac{1+{k}^{2}}{2{k}^{2}-1}$.…(13分)
设O到直线MN的距离为d,因为(|OM|2+|ON|2)d2=|OM|2|ON|2,
所以$\frac{1}{{d}^{2}}$=$\frac{1}{|OM{|}^{2}}$+$\frac{1}{|ON{|}^{2}}$=3,即d=$\frac{\sqrt{3}}{3}$.
综上,O到直线MN的距离是定值.…(16分)
点评 本题考查直线与圆锥曲线的综合问题,圆锥曲线的综合,向量的数量积的应用,设而不求的解题方法,点到直线的距离的应用,考查分析问题解决问题的能力,考查计算能力.


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,4) | B. | (4,5) | C. | (1,5) | D. | (5,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{6}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
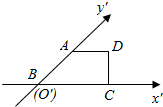 有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图)∠ABC=45°,AB=$\sqrt{2}$,AD=1,DC⊥BC,则这块菜地的面积为$3\sqrt{2}$.
有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图)∠ABC=45°,AB=$\sqrt{2}$,AD=1,DC⊥BC,则这块菜地的面积为$3\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com