
【题目】已知函数![]() .
.
(1)当a=![]() 时,试判断函数f(x)的单调性;
时,试判断函数f(x)的单调性;
(2)设g(x)=![]() ,若g(x)有唯一零点,求实数a的取值范围.
,若g(x)有唯一零点,求实数a的取值范围.
【答案】(1)f(x)在(0,+∞)上单调递减.(2)![]() .
.
【解析】
(1)求出![]() ,两次求导,可判断在区间
,两次求导,可判断在区间![]()
![]() 恒成立,从而可得结果;(2)g(x)=
恒成立,从而可得结果;(2)g(x)=![]() ,x>0,g(x)=
,x>0,g(x)=![]() +2ax,分四种情况讨论,分别利用导数研究函数的单调性,求出函数的极值,结合单调性与极值分别判断是否符合题意,从而得到实数a的取值范围.
+2ax,分四种情况讨论,分别利用导数研究函数的单调性,求出函数的极值,结合单调性与极值分别判断是否符合题意,从而得到实数a的取值范围.
(1)当a=![]() 时,f(x)=
时,f(x)=![]() ,x>0,
,x>0,
求导得![]() ,令p(x)=
,令p(x)=![]() ,则p(x)=
,则p(x)=![]() ,
,
当x>1时,p(x)<0,当0<x<1时,p(x)>0,
所以f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
所以f(x)≤f(1)=0,当且仅当x=1时,等号成立,
所以f(x)在(0,+∞)上单调递减.
(2)g(x)=![]() ,x>0,g(x)=
,x>0,g(x)=![]() +2ax,
+2ax,
①当a≥0时,g(x)>0,g(x)在(0,+∞)上单调递增,
因为g(1)=0,所以g(x)有唯一零点.
②当a=![]() 时,g(x)=
时,g(x)=![]() ,
,
当0<x<1时,g(x)>0,当x>1时,g(x)<0,
则g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
因为g(1)=0,所以g
③当![]() <a<0时,由g(x)=0,得x=
<a<0时,由g(x)=0,得x=![]() >1,
>1,
当0<x<![]() 时,g(x)>0,当x>
时,g(x)>0,当x>![]() 时,g(x)<0,
时,g(x)<0,
则g(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减,
,+∞)上单调递减,
因为g(1)=0,所以g(![]() )>0,
)>0,
由(1)可知,lnx≤![]() ,当且仅当x=1时等号成立,
,当且仅当x=1时等号成立,
因为![]() >
>![]() >1(注:因为
>1(注:因为![]() <a<0,所以
<a<0,所以![]() ,所以
,所以![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以![]() ,所以
,所以![]() >
>![]() >1),
>1),
且![]() ,
,
所以g(x)在(![]() ,
,![]() )上存在一个零点,
)上存在一个零点,
即g(x)存在两个零点,不符合题意.
④当a<![]() 时,由g(x)=0,得x=
时,由g(x)=0,得x=![]() <1,
<1,
当0<x<![]() 时,g(x)>0,当x>
时,g(x)>0,当x>![]() 时,g(x)<0,
时,g(x)<0,
则g(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减,
,+∞)上单调递减,
因为g(1)=0,所以g(![]() )>0,
)>0,
令h(x)=xex+1,h(x)=(x+1)ex,
易知h(x)在![]() 上单调递减,则在
上单调递减,则在![]() 上h(x)>
上h(x)>![]() =1-
=1-![]() >0.
>0.
因为a<![]() ,所以2a<
,所以2a<![]() ,所以h(2a)=2ae2a+1>0,即ea<
,所以h(2a)=2ae2a+1>0,即ea<![]() <1,
<1,
此时g(ea)=![]() =ae2a<0,
=ae2a<0,
所以g(x)在(ea,![]() )上存在一个零点,且g(1)=0,
)上存在一个零点,且g(1)=0,
即g(x)存在两个零点,不符合题意.
综上所述,若g(x)有唯一零点,则实数a的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图几何体是圆锥的一部分,它是Rt△ABC(及其内部)以一条直角边AB所在直线为旋转轴旋转150°得到的,AB=BC=2,P是弧![]() 上一点,且EB⊥AP.
上一点,且EB⊥AP.
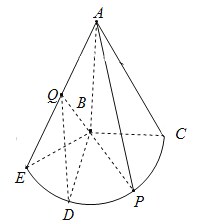
(1)求∠CBP的大小;
(2)若Q为AE的中点,D为弧![]() 的中点,求二面角Q﹣BD﹣P的余弦值;
的中点,求二面角Q﹣BD﹣P的余弦值;
(3)直线AC上是否存在一点M,使得B、D、M、Q四点共面?若存在,请说明点M的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,小刘从各个渠道融资
日,小刘从各个渠道融资![]() 万元,在某大学投资一个咖啡店,
万元,在某大学投资一个咖啡店,![]() 年
年![]() 月
月![]() 日正式开业,已知开业第一年运营成本为
日正式开业,已知开业第一年运营成本为![]() 万元,由于工人工资不断增加及设备维修等,以后每年成本增加
万元,由于工人工资不断增加及设备维修等,以后每年成本增加![]() 万元,若每年的销售额为
万元,若每年的销售额为![]() 万元,用数列
万元,用数列![]() 表示前
表示前![]() 年的纯收入.(注:纯收入
年的纯收入.(注:纯收入![]() 前
前![]() 年的总收入
年的总收入![]() 前
前![]() 年的总支出
年的总支出![]() 投资额)
投资额)
(1)试求年平均利润最大时的年份(年份取正整数)并求出最大值.
(2)若前![]() 年的收入达到最大值时,小刘计划用前
年的收入达到最大值时,小刘计划用前![]() 年总收入的
年总收入的![]() 对咖啡店进行重新装修,请问:小刘最早从哪一年对咖啡店进行重新装修(年份取整数)?并求小刘计划装修的费用.
对咖啡店进行重新装修,请问:小刘最早从哪一年对咖啡店进行重新装修(年份取整数)?并求小刘计划装修的费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由0,1,2,3,4,5,6,7,8,9组成没有重复数字的五位数,且是奇数,其中恰有两个数字是偶数,则这样的五位数的个数为( ).
A.7200B.6480C.4320D.5040
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年暑期都会有大量中学生参加名校游学,夏令营等活动,某中学学生社团将其今年的社会实践主题定为“中学生暑期游学支出分析”,并在该市各个中学随机抽取了共![]() 名中学生进行问卷调查,根据问卷调查发现共
名中学生进行问卷调查,根据问卷调查发现共![]() 名中学生参与了各类游学、夏令营等活动,从中统计得到中学生暑期游学支出(单位:百元)频率分布方图如图.
名中学生参与了各类游学、夏令营等活动,从中统计得到中学生暑期游学支出(单位:百元)频率分布方图如图.
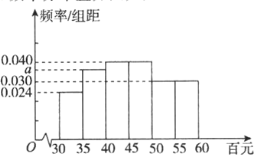
(I)求实数![]() 的值;
的值;
(Ⅱ)在![]() ,
,![]() ,
,![]() 三组中利用分层抽样抽取
三组中利用分层抽样抽取![]() 人,并从抽取的
人,并从抽取的![]() 人中随机选出
人中随机选出![]() 人,对其消费情况进行进一步分析.
人,对其消费情况进行进一步分析.
(i)求每组恰好各被选出![]() 人的概率;
人的概率;
(ii)设![]() 为选出的
为选出的![]() 人中
人中![]() 这一组的人数,求随机变量
这一组的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省数学学会为选拔一批学生代表该省参加全国高中数学联赛,在省内组织了一次预选赛,该省各校学生均可报名参加.现从所有参赛学生中随机抽取![]() 人的成绩进行统计,发现这
人的成绩进行统计,发现这![]() 名学生中本次预选赛成绩优秀的男、女生人数之比为
名学生中本次预选赛成绩优秀的男、女生人数之比为![]() ,成绩一般的男、女生人数之比为
,成绩一般的男、女生人数之比为![]() .已知从这
.已知从这![]() 名学生中随机抽取一名学生,抽到男生的概率是
名学生中随机抽取一名学生,抽到男生的概率是![]()
(1)请将下表补充完整,并判断是否有![]() 的把握认为在本次预选赛中学生的成绩优秀与性别有关?
的把握认为在本次预选赛中学生的成绩优秀与性别有关?
成绩优秀 | 成绩一般 | 总计 | |
男生 | |||
女生 | |||
总计 |
|
(2)以样本估计总体,视样本频率为相应事件发生的概率,从所有本次预选赛成绩优秀的学生中随机抽取![]() 人代表该省参加全国联赛,记抽到的女生人数为
人代表该省参加全国联赛,记抽到的女生人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: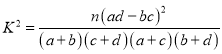 ,其中
,其中![]() ;
;
临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】黄河被称为我国的母亲河,它的得名据说来自于河水的颜色,黄河因携带大量泥沙所以河水呈现黄色, 黄河的水源来自青海高原,上游的1000公里的河水是非常清澈的.只是中游流经黄土高原,又有太多携带有大量泥沙的河流汇入才造成黄河的河水逐渐变得浑浊.在刘家峡水库附近,清澈的黄河和携带大量泥沙的洮河汇合,在两条河流的交汇处,水的颜色一清一浊,互不交融,泾渭分明,形成了一条奇特的水中分界线,设黄河和洮河在汛期的水流量均为2000![]() ,黄河水的含沙量为
,黄河水的含沙量为![]() ,洮河水的含沙量为
,洮河水的含沙量为![]() ,假设从交汇处开始沿岸设有若干个观测点,两股河水在流经相邻的观测点的过程中,其混合效果相当于两股河水在1秒内交换
,假设从交汇处开始沿岸设有若干个观测点,两股河水在流经相邻的观测点的过程中,其混合效果相当于两股河水在1秒内交换![]() 的水量,即从洮河流入黄河
的水量,即从洮河流入黄河![]() 的水混合后,又从黄河流入
的水混合后,又从黄河流入![]() 的水到洮河再混合.
的水到洮河再混合.

(1)求经过第二个观测点时,两股河水的含沙量;
(2)从第几个观测点开始,两股河水的含沙量之差小于![]() ?(不考虑泥沙沉淀)
?(不考虑泥沙沉淀)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com