
分析 ①设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),由离心率可得a=b,c=$\sqrt{2}$a,再由焦点到渐近线的距离可得c,进而得到a,b和双曲线的方程;
②直线与双曲线方程联立消去y,设A(x1,y1)、B(x2,y2),进而根据判别大于0及x1和x2的范围求得k的范围,表示出AB中点的坐标,进而表示出直线l的方程,令x=0求得m关于k的表达式,根据k的范围求得m的范围.
解答 解:①设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),
由e=$\frac{c}{a}$=$\sqrt{1+(\frac{b}{a})^{2}}$=$\sqrt{2}$,可得a=b,c=$\sqrt{2}$a,
由焦点(c,0)到一条渐近线y=x的距离为1,
可得$\frac{c}{\sqrt{2}}$=1,即c=$\sqrt{2}$,a=b=1.
则双曲线的方程为x2-y2=1;
②由$\left\{\begin{array}{l}{y=kx+1}\\{{x}^{2}-{y}^{2}=1}\end{array}\right.$,得(1-k2)x2-2kx-2=0,
设A(x1,y1)、B(x2,y2),
则$\left\{\begin{array}{l}{△=4{k}^{2}+8(1-{k}^{2})>0}\\{{x}_{1}+{x}_{2}=\frac{2k}{1-{k}^{2}}<0}\\{{x}_{1}{x}_{2}=\frac{2}{{k}^{2}-1}>0}\end{array}\right.$,解得1<k<$\sqrt{2}$,
∴AB中点E为($\frac{k}{1-{k}^{2}}$,$\frac{1}{1-{k}^{2}}$),
又F(-$\sqrt{2}$,0),
∴直线EF方程为y=$\frac{1}{k+\sqrt{2}-\sqrt{2}{k}^{2}}$(x+$\sqrt{2}$),
令x=0,
得m=$\frac{\sqrt{2}}{k+\sqrt{2}-\sqrt{2}{k}^{2}}$=$\frac{1}{-{k}^{2}+\frac{\sqrt{2}}{2}k+1}$
=$\frac{1}{-(k-\frac{\sqrt{2}}{4})^{2}+\frac{7}{8}}$,
由1<k<$\sqrt{2}$,可得m>$\sqrt{2}$.
所以m的范围是($\sqrt{2}$,+∞).
点评 本题考查双曲线的方程的求法,考查了直线与双曲线的综合问题.用k表示m的过程即是建立目标函数的过程,本题要注意k的取值范围.


科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①③ | C. | ①② | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
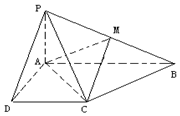 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且$PA=AD=DC=\frac{1}{2}$,AB=1,M是PB的中点
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且$PA=AD=DC=\frac{1}{2}$,AB=1,M是PB的中点 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 4 | 5 | 6 | 7 |
| y | 8.2 | 7.8 | 6.6 | 5.4 |
| A. | -0.92 | B. | -0.94 | C. | -0.96 | D. | -0.98 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com