【题目】若四面体
的三组对棱分别相等，即
给出下列结论：
①四面体
每个面的面积相等；
②从四面体
每个顶点出发的三条棱两两夹角之和大于
而小于
；
③连结四面体
每组对棱中点的线段相互垂直平分；
④从四面体
每个顶点出发的三条棱的长可作为一个三角形的三边长；
其中正确结论的序号是__________。（写出所有正确结论的序号）
53随堂测系列答案科目：高中数学 来源： 题型：
【题目】如图所示，空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA上的点，且满足
．
(1)求证：四边形EFGH是梯形；
(2)若BD＝a，求梯形EFGH的中位线的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个盒中装有编号分别为1,2,3,4的四个形状大小完全相同的小球.
（1）从盒中任取两球，求取出的球的编号之和大于5的概率.
（2）从盒中任取一球，记下该球的编号
，将球放回，再从盒中任取一球，记下该球的编号
，求
的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1，在高为2的梯形
中， 
， 
， 
，过
、
分别作
， 
，垂足分别为
、
。已知
，将梯形
沿
、
同侧折起，得空间几何体
，如图2。
（1）若
，证明： 
；
（2）若
，证明： 
；
（3）在（1），（2）的条件下，求三棱锥
的体积。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校高三共有2000名学生参加广安市联考，现随机抽取100名学生的成绩（单位：分），并列成如下表所示的频数分布表：
组别 |
|
|
|
|
|
|
频数 | 6 | 18 | 28 | 26 | 17 | 5 |
（1）试估计该年级成绩
分的学生人数；
（2）已知样本中成绩在
中的6名学生中，有4名男生，2名女生，现从中选2人进行调研，求恰好选中一名男生一名女生的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一盒中装有12个球，其中5个红球，4个黑球，2个白球，1个绿球．从中随机取出1球，求：
(1)取出1球是红球或黑球的概率；
(2)取出1球是红球或黑球或白球的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知中国某手机品牌公司生产某款手机的年固定成本为40万元，每生产1万部还需另投入16万元．设公司一年内共生产该款手机
万部并全部销量完，每万部的销售收入为
万元，且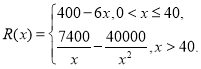
（1）写出年利润
万元关于年产量
（万部）的函数解析式；
（2）当年产量为多少万部时，公司在该款手机的生产中所获得的利润最大？并求出最大利润．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
