
【题目】已知函数f(x)=2 ![]() .
.
(1)求函数f(x)的定义域和值域;
(2)求函数f(x)的单调区间.
【答案】
(1)解:对于函数f(x)=2 ![]() ,
,
令t=x2﹣2x﹣3=(x﹣1)2﹣4≥﹣4,可得f(x)=g(t)=2t (t≥﹣4).
由于t的定义域为R,故故函数的定义域为R.
∵t≥﹣4,故f(x)≥2﹣4= ![]() ,故f(x)的值域为[
,故f(x)的值域为[ ![]() ,+∞).
,+∞).
(2)解:根据f(x)=g(t)=2t,函数f(x)的单调区间,即函数t的单调区间.
由于函数t=(x﹣1)2﹣4的减区间为(﹣∞,1],增区间为:[1,+∞),
故函数f(x)的单调递减区间:(﹣∞,1],单调递增区间:[1,+∞)
【解析】(1)令t=x2﹣2x﹣3,f(x)=g(t)=2t (t≥﹣4),利用二次函数的性质求得t的定义域与值域,可得函数f(x)的定义域和值域.(2)函数f(x)的单调区间,即函数t的单调区间,再利用二次函数的性质得出结论.
【考点精析】关于本题考查的函数的定义域及其求法和函数的值域,需要了解求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能得出正确答案.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】空间四边形PABC的各边及对角线长度都相等,D、E、F、G分别是AB、BC、CA、AP的中点,下列四个结论中成立的是
①BC∥平面PDF
②DF⊥平面PAE
③平面GDF∥平面PBC
④平面PAE⊥平面ABC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在实数集
在实数集![]() 上的图象是连续不断的,且对任意实数
上的图象是连续不断的,且对任意实数![]() 存在常数
存在常数![]() 使得
使得![]() 恒成立,则称
恒成立,则称![]() 是一个“关于
是一个“关于![]() 函数”.现有下列“关于
函数”.现有下列“关于![]() 函数”的结论:
函数”的结论:
①常数函数是“关于![]() 函数”;
函数”;
②正比例函数必是一个“关于![]() 函数”;
函数”;
③“关于![]() 函数”至少有一个零点;
函数”至少有一个零点;
④![]() 是一个“关于
是一个“关于![]() 函数”.
函数”.
其中正确结论的序号是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系下,已知圆O:ρ=cosθ+sinθ和直线l:ρsin(θ﹣ ![]() )=
)= ![]() .
.
(1)求圆O和直线l的直角坐标方程;
(2)当θ∈(0,π)时,求直线l与圆O公共点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题是全称命题还是特称命题,并判断其真假.
(1)对数函数都是单调函数;
(2)至少有一个整数,它既能被11整除,又能被9整除;
(3)x∈{x|x>0}, ![]() ;
;
(4)x0∈Z,log2x0>2.
查看答案和解析>>
科目:高中数学 来源: 题型:
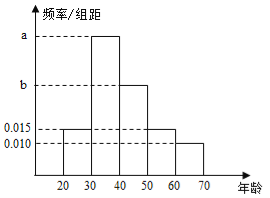
【题目】【广西南宁2017届高三检测】根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图.
(1)已知![]() 、
、![]() ,
,![]() 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求![]() ,
,![]() 的值;
的值;
(2)该电子商务平台将年龄在![]() 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放80元的代金券,已经采用分层抽样的方式从参与调查的1000位上网购物者中抽取了10人,现在要在这10人中随机抽取3人进行回访,求此三人获得代金券总和
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放80元的代金券,已经采用分层抽样的方式从参与调查的1000位上网购物者中抽取了10人,现在要在这10人中随机抽取3人进行回访,求此三人获得代金券总和![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,点![]() (n∈N*)均在函数y=3x-2的图象上.
(n∈N*)均在函数y=3x-2的图象上.
(1)求数列{an}的通项公式;
(2)设bn=![]() ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn<![]() 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
整理评分数据,将分数以![]() 为组距分成
为组距分成![]() 组:
组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
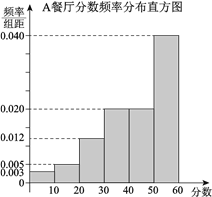
B餐厅分数频数分布表 | |
分数区间 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
定义学生对餐厅评价的“满意度指数”如下:
分数 |
|
|
|
满意度指数 |
|
|
|
(Ⅰ)在抽样的100人中,求对A餐厅评价“满意度指数”为![]() 的人数;
的人数;
(Ⅱ)从该校在A,B两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某钢厂打算租用![]() ,
, ![]() 两种型号的火车车皮运输900吨钢材,
两种型号的火车车皮运输900吨钢材, ![]() ,
, ![]() 两种车皮的载货量分别为36吨和60吨,租金分别为1.6万元/个和2.4万元/个,钢厂要求租车皮总数不超过21个,且
两种车皮的载货量分别为36吨和60吨,租金分别为1.6万元/个和2.4万元/个,钢厂要求租车皮总数不超过21个,且![]() 型车皮不多于
型车皮不多于![]() 型车皮7个,分别用
型车皮7个,分别用![]() ,
, ![]() 表示租用
表示租用![]() ,
, ![]() 两种车皮的个数.
两种车皮的个数.
(Ⅰ)用![]() ,
, ![]() 列出满足条件的数学关系式,并画出相应的平面区域;
列出满足条件的数学关系式,并画出相应的平面区域;
(Ⅱ)分别租用![]() ,
, ![]() 两种车皮的个数是多少时,才能使得租金最少?并求出此最小租金.
两种车皮的个数是多少时,才能使得租金最少?并求出此最小租金.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com