

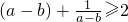
 (当且仅当a=b时取“=”号),而a、b是互不相等的正数,故正确;
(当且仅当a=b时取“=”号),而a、b是互不相等的正数,故正确; (a2+b2+c2+a2+b2+c2)
(a2+b2+c2+a2+b2+c2) (2ab+2ca+2bc)=ab+bc+ca,而a、b、c是互不相等的正数,故正确;
(2ab+2ca+2bc)=ab+bc+ca,而a、b、c是互不相等的正数,故正确;

科目:高中数学 来源:2013届安徽省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
已知a、b、c是互不相等的非零实数.若用反证法证明三个方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+b=0至少有一个方程有两个相异实根.
【解析】本试题主要考查了二次方程根的问题的综合运用。运用反证法思想进行证明。
先反设,然后推理论证,最后退出矛盾。证明:假设三个方程中都没有两个相异实根,
则Δ1=4b2-4ac≤0,Δ2=4c2-4ab≤0,Δ3=4a2-4bc≤0
相加有a2-2ab+b2+b2-2bc+c2+c2-2ac+a2≤0,
(a-b)2+(b-c)2+(c-a)2≤0.显然不成立。
证明:假设三个方程中都没有两个相异实根,
则Δ1=4b2-4ac≤0,Δ2=4c2-4ab≤0,Δ3=4a2-4bc≤0.
相加有a2-2ab+b2+b2-2bc+c2+c2-2ac+a2≤0,
(a-b)2+(b-c)2+(c-a)2≤0. ①
由题意a、b、c互不相等,∴①式不能成立.
∴假设不成立,即三个方程中至少有一个方程有两个相异实根.
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com