
ЁОЬтФПЁПЁАПТЮїВЛЕШЪНЁБЪЧгЩЪ§бЇМвПТЮїдкбаОПЪ§бЇЗжЮіжаЕФЁАСїЪ§ЁБЮЪЬтЪБЕУЕНЕФЃЌЕЋДгРњЪЗЕФНЧЖШНВЃЌИУВЛЕШЪНгІЕБГЦЮЊПТЮїЉЉВМФсбЧПЦЗђЫЙЛљЉЉЪЉЭпДФВЛЕШЪНЃЌвђЮЊе§ЪЧКѓСНЮЛЪ§бЇМвБЫДЫЖРСЂЕидкЛ§ЗжбЇжаЭЦЖјЙужЎЃЌВХНЋетвЛВЛЕШЪНЭЦЙуЕНЭъЩЦЕФЕиВНЃЌдкИпжаЪ§бЇбЁаоНЬВФ4Љ5жаИјГіСЫЖўЮЌаЮЪНЕФПТЮїВЛЕШЪНЃКЃЈa2+b2ЃЉЃЈc2+d2ЃЉЁнЃЈac+bdЃЉ2ЕБЧвНіЕБadЃНbcЃЈМД![]() ЃЉЪБЕШКХГЩСЂЃЎИУВЛЕШЪНдкЪ§бЇжажЄУїВЛЕШЪНКЭЧѓКЏЪ§зюжЕЕШЗНУцЖМгаЙуЗКЕФгІгУЃЎИљОнПТЮїВЛЕШЪНПЩжЊКЏЪ§
ЃЉЪБЕШКХГЩСЂЃЎИУВЛЕШЪНдкЪ§бЇжажЄУїВЛЕШЪНКЭЧѓКЏЪ§зюжЕЕШЗНУцЖМгаЙуЗКЕФгІгУЃЎИљОнПТЮїВЛЕШЪНПЩжЊКЏЪ§![]() ЕФзюДѓжЕМАШЁЕУзюДѓжЕЪБxЕФжЕЗжБ№ЮЊЃЈЁЁЁЁЃЉ
ЕФзюДѓжЕМАШЁЕУзюДѓжЕЪБxЕФжЕЗжБ№ЮЊЃЈЁЁЁЁЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 гХвэаЁАяЪжЭЌВНПкЫуЯЕСаД№АИ
гХвэаЁАяЪжЭЌВНПкЫуЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ

ЃЈ1ЃЉжЄУїЃК![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉдкЯпЖЮ![]() ЩЯЃЌЪЧЗёДцдквЛЕу
ЩЯЃЌЪЧЗёДцдквЛЕу![]() ЃЌЪЙЕУЖўУцНЧ
ЃЌЪЙЕУЖўУцНЧ![]() ЕФДѓаЁЮЊ
ЕФДѓаЁЮЊ![]() ЃПШчЙћДцдкЃЌЧѓ
ЃПШчЙћДцдкЃЌЧѓ![]() ЕФжЕЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФжЕЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшвЛИіДќзгРягаКьЁЂЛЦЁЂРЖЩЋаЁЧђИївЛИіЯжУПДЮДгДќзгРяШЁГівЛИіЧђ(ШЁГіФГЩЋЧђЕФИХТЪОљЯрЭЌ)ЃЌШЗЖЈбеЩЋКѓЗХЛиЃЌжБЕНСЌајСНДЮОљШЁГіКьЩЋЧђЪБЮЊжЙЃЌМЧДЫЪБШЁГіЧђЕФДЮЪ§ЮЊІЮЃЌдђІЮЕФЪ§бЇЦкЭћЮЊ_____ .
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФПЧАЃЌЧрняЫизїЮЊвЛЯпПЙХБвЉЦЗЕУЕНДѓСІЭЦЙуФГХЉПЦЫљЮЊСЫЩюШыбаОПКЃАЮвђЫиЖдЧрняЫиВњСПЕФгАЯьЃЌдкЩНЩЯКЭЩНЯТЕФЪдбщЬяжаЗжБ№жжжВСЫ![]() жъЧрняНјааЖдБШЪдбщ.ЯждкДгЩНЩЯКЭЩНЯТЕФЪдбщЬяжаИїЫцЛњбЁШЁСЫ
жъЧрняНјааЖдБШЪдбщ.ЯждкДгЩНЩЯКЭЩНЯТЕФЪдбщЬяжаИїЫцЛњбЁШЁСЫ![]() жъЧрнязїЮЊбљБОЃЌУПжъЬсШЁЕФЧрняЫиВњСПЃЈЕЅЮЛЃКПЫЃЉШчЯТБэЫљЪОЃК
жъЧрнязїЮЊбљБОЃЌУПжъЬсШЁЕФЧрняЫиВњСПЃЈЕЅЮЛЃКПЫЃЉШчЯТБэЫљЪОЃК
БрКХЮЛжУ | Ђй | Ђк | Ђл | Ђм |
ЩНЩЯ |
|
|
|
|
ЩНЯТ |
|
|
|
|
ЃЈ1ЃЉИљОнбљБОЪ§ОнЃЌЪдЙРМЦЩНЯТЪдбщЬяЧрняЫиЕФзмВњСПЃЛ
ЃЈ2ЃЉМЧЩНЩЯгыЩНЯТСНПщЪдбщЬяЕЅжъЧрняЫиВњСПЕФЗНВюЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌИљОнбљБОЪ§ОнЃЌЪдЙРМЦ
ЃЌИљОнбљБОЪ§ОнЃЌЪдЙРМЦ![]() гы
гы![]() ЕФДѓаЁЙиЯЕЃЈжЛашаДГіНсТлЃЉЃЛ
ЕФДѓаЁЙиЯЕЃЈжЛашаДГіНсТлЃЉЃЛ
ЃЈ3ЃЉДгбљБОжаЕФЩНЩЯгыЩНЯТЧрняжаИїЫцЛњбЁШЁ![]() жъЃЌМЧет
жъЃЌМЧет![]() жъЕФВњСПзмКЭЮЊ
жъЕФВњСПзмКЭЮЊ![]() ЕФИХТЪ.
ЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖPЃABCDжаЃЌЕзУцABCDЮЊжБНЧЬнаЮЃЌABЁЮCDЃЌABЁЭADЃЌPAЁЭЦНУцABCDЃЌEЪЧРтPCЩЯвЛЕу.

ЃЈ1ЃЉжЄУїЃКЦНУцADEЁЭЦНУцPAB.
ЃЈ2ЃЉШєPEЃН4ECЃЌOЮЊЕуEдкЦНУцPABЩЯЕФЭЖгАЃЌ![]() ЃЌABЃНAPЃН2CDЃН2ЃЌЧѓЫФРтзЖPЃADEOЕФЬхЛ§.
ЃЌABЃНAPЃН2CDЃН2ЃЌЧѓЫФРтзЖPЃADEOЕФЬхЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЧњЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ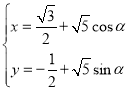 ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌвдЦНУцжБНЧзјБъЯЕЕФдЕуЮЊМЋЕуЃЌ
ЮЊВЮЪ§ЃЉЃЌвдЦНУцжБНЧзјБъЯЕЕФдЕуЮЊМЋЕуЃЌ![]() жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎ
жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎ
ЃЈ1ЃЉНЋЧњЯп![]() ЕФВЮЪ§ЗНГЬЛЏЮЊМЋзјБъЗНГЬЃЛ
ЕФВЮЪ§ЗНГЬЛЏЮЊМЋзјБъЗНГЬЃЛ
ЃЈ2ЃЉЩшжБЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ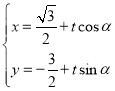 ЃЈЦфжа
ЃЈЦфжа![]() ЮЊВЮЪ§ЃЉЃЌШє
ЮЊВЮЪ§ЃЉЃЌШє![]() гыЧњЯп
гыЧњЯп![]() ЯрНЛгк
ЯрНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЧв
СНЕуЃЌЧв![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() ЕФаБТЪЃЎ
ЕФаБТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЕФзюаЁе§жмЦкЮЊ
ЕФзюаЁе§жмЦкЮЊ![]() ЃЌЦфЭМЯѓЙигкжБЯп
ЃЌЦфЭМЯѓЙигкжБЯп![]() ЖдГЦЃЎИјГіЯТУцЫФИіНсТлЃКЂйНЋ
ЖдГЦЃЎИјГіЯТУцЫФИіНсТлЃКЂйНЋ![]() ЕФЭМЯѓЯђгвЦНвЦ
ЕФЭМЯѓЯђгвЦНвЦ![]() ИіЕЅЮЛГЄЖШКѓЕУЕНКЏЪ§ЭМЯѓЙигкдЕуЖдГЦЃЛЂкЕу
ИіЕЅЮЛГЄЖШКѓЕУЕНКЏЪ§ЭМЯѓЙигкдЕуЖдГЦЃЛЂкЕу![]() ЮЊ
ЮЊ![]() ЭМЯѓЕФвЛИіЖдГЦжааФЃЛЂл
ЭМЯѓЕФвЛИіЖдГЦжааФЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() дкЧјМф
дкЧјМф![]() ЩЯЕЅЕїЕндіЃЎЦфжае§ШЗЕФНсТлЮЊЃЈ ЃЉ
ЩЯЕЅЕїЕндіЃЎЦфжае§ШЗЕФНсТлЮЊЃЈ ЃЉ
A.ЂйЂкB.ЂкЂлC.ЂкЂмD.ЂйЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌ
ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌ![]() жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп
жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓжБЯп![]() ЕФЦеЭЈЗНГЬКЭЧњЯп
ЕФЦеЭЈЗНГЬКЭЧњЯп![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉЩшЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() гыЧњЯп
гыЧњЯп![]() НЛгк
НЛгк![]() СНЕуЃЌЧѓ
СНЕуЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2013ФъЛЊШЫЪ§бЇМвеХвцЬЦжЄУїСЫТЯЩњЫиЪ§ВТЯыЕФвЛИіШѕЛЏаЮЪНЃЌДЫЪТв§Ц№СЫЙњМЪЪ§бЇНчЕФКфЖЏаэЖрзЈМвШЯЮЊетЪЧЪ§ТлбаОПжаЕФвЛЯюжиДѓЭЛЦЦЪРНчжїСїУНЬхЖМЖдетЯюживЊГЩЙћзїСЫБЈЕРВЂИјгшСЫИпЖШЦРМлЃЌгЁЖШУНЬхЩѕжСГЦдоеХвцЬЦЮЊЁАжаЙњЕФРТэХЌН№ЁБ.ТЯЩњЫиЪ§ВТЯыЪЧЯЃЖћВЎЬидк1900ФъЬсГіЕФ23ИіЮЪЬтжЎвЛЃЌПЩвдетбљУшЪіЃКДцдкЮоЧюЖрИіЫиЪ§![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЪЧЫиЪ§ЃЌЫиЪ§Жд
ЪЧЫиЪ§ЃЌЫиЪ§Жд![]() ГЦЮЊТЯЩњЫиЪ§.дкВЛГЌЙ§20ЕФЫиЪ§жаЃЌЫцЛњбЁШЁСНИіВЛЭЌЕФЪ§ЃЌЦфжаФмЙЛзщГЩТЯЩњЫиЪ§ЕФИХТЪЪЧЃЈ ЃЉ
ГЦЮЊТЯЩњЫиЪ§.дкВЛГЌЙ§20ЕФЫиЪ§жаЃЌЫцЛњбЁШЁСНИіВЛЭЌЕФЪ§ЃЌЦфжаФмЙЛзщГЩТЯЩњЫиЪ§ЕФИХТЪЪЧЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com