
【题目】已知函数f(x)=mlnx﹣x2+2(m∈R).
(1)当m=1时,求f(x)的单调区间;
(2)若f(x)在x=1时取得极大值,求证:f(x)﹣f′(x)≤4x﹣3;
(3)若m≤8,当x≥1时,恒有f(x)﹣f′(x)≤4x﹣3恒成立,求m的取值范围.
【答案】
(1)解:f(x)的定义域为(0,+∞), ![]() ,
,
解f′(x)=0,得 ![]() .当
.当 ![]() 时,f′(x)>0,f(x)单调递增;
时,f′(x)>0,f(x)单调递增;
当 ![]() 时,f′(x)<0,f(x)单调递减.
时,f′(x)<0,f(x)单调递减.
综上,当m=1时,f(x)在 ![]() 上单调递增,在
上单调递增,在 ![]() 上单调递减.
上单调递减.
(2)解:若f(x)在x=1时取得极大值,则 ![]() ,则m=2.
,则m=2.
此时f(x)=2lnx﹣x2+2, ![]() .
.
令g(x)=f(x)﹣f′(x)﹣4x+3,
则 ![]() .
. ![]() .
.
令g′(x)=0,得x=±1.列表得
x | (0,1) | 1 | (1,+∞) |
g′(x) | + | 0 | ﹣ |
g(x) | ↗ | 极大值 | ↘ |
…(8分)
由上表知,gmax(x)=g(1)=0,所以g(x)≤0,即f(x)﹣f′(x)≤4x﹣3.
(3)解:令 ![]()
则 ![]() ①.
①.
当m≤2时,g′(x)<0,所以g(x)在(1,+∞)上单调递减,所以当x≥1,g(x)≤
g(1),
故只需g(1)≤0,即﹣1﹣2﹣m+5≤0,即m≥2,所以m=2.
②当2<m≤8时,解g′(x)=0,得 ![]() .
.
当 ![]() 时,g′(x)>0,g(x)单调递增;
时,g′(x)>0,g(x)单调递增;
当 ![]() 时,g′(x)<0,g(x)单调递减.
时,g′(x)<0,g(x)单调递减.
所以当 ![]() 时,g(x)取得最大值.
时,g(x)取得最大值.
故只需 ![]() ,即
,即 ![]() ,
,
令 ![]() ,则
,则 ![]() ,
, ![]() ,
,
所以h′(x)在(1,+∞)上单调递增,
又h′(1)=﹣2<0,h′(4)=ln4﹣1>0,以x0∈(1,4),h′(x0)=0,
所以h(x)在(1,x0)上单调递减,
在(x0,4)上递增,而h(1)=﹣1﹣4+5=0,h(4)=4ln4﹣4﹣8+5=8ln2﹣7<0,
所以x∈[1,4]上恒有h(x)≤0,
所以当2<m≤8时, ![]() .
.
综上所述,2≤m≤8.
【解析】(1)f(x)的定义域为(0,+∞),求出函数的导数,利用f′(x)=0,求出极值点判断函数的单调性,求出单调区间.(2)利用f(x)在x=1时取得极大值,求出m,令g(x)=f(x)﹣f′(x)﹣4x+3,通过函数的导数,求出函数的最值即可.(3)令 ![]() ,求出导函数,通过当m≤2时,g′(x)<0,当2<m≤8时,求出g(x)取得最大值.然后求解2≤m≤8.
,求出导函数,通过当m≤2时,g′(x)<0,当2<m≤8时,求出g(x)取得最大值.然后求解2≤m≤8.
【考点精析】关于本题考查的利用导数研究函数的单调性和函数的极值与导数,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能得出正确答案.
是极小值才能得出正确答案.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
, ![]() ,其中
,其中![]() .
.
(1)设![]() ,求证:数列
,求证:数列![]() 是等差数列,并求出
是等差数列,并求出![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 对于
对于![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
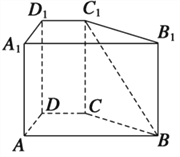
【题目】如图,已知直四棱柱ABCD—A1B1C1D1中,AA1=2,底面ABCD是直角梯形,∠A为直角,AB∥CD,AB=4,AD=2,DC=2.
(Ⅰ)求线段BC1的长度;
(Ⅱ)异面直线BC1与DC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+(lga+2)x+lgb满足f(﹣1)=﹣2且对于任意x∈R,恒有f(x)≥2x成立.
(1)求实数a,b的值;
(2)解不等式f(x)<x+5.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,M、N分别为棱BC和棱CC1的中点,则异面直线AC和MN所成的角为( )
A. 30° B. 45° C. 90° D. 60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() cos(2x-
cos(2x-![]() ),x∈R.
),x∈R.
(1)求函数f(x)的最小正周期和单调递减区间;
(2)求函数f(x)在区间[-![]() ,
,![]() ]上的最小值和最大值,并求出取得最值时x的值.
]上的最小值和最大值,并求出取得最值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查甲、乙两种品牌商品的市场认可度,在某购物网点随机选取了14天,统计在某确定时间段的销量,得如下所示的统计图,根据统计图求:
(1)甲、乙两种品牌商品销量的中位数分别是多少?
(2)甲品牌商品销量在[20,50]间的频率是多少?
(3)甲、乙两个品牌商品哪个更受欢迎?并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的焦点是椭圆
的焦点是椭圆![]() 的顶点,
的顶点, ![]() 为椭圆
为椭圆![]() 的左焦点且椭圆
的左焦点且椭圆![]() 经过点
经过点 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右顶点
的右顶点![]() 作斜率为
作斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于另一点
于另一点![]() ,连结
,连结![]() 并延长
并延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,当
,当![]() 的面积取得最大值时,求
的面积取得最大值时,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com